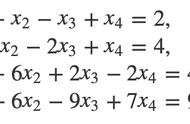顾名思义,特值法就是找一些符合题目要求的特殊条件解题。
例:f(n)=(n 1)^n-1(n为自然数且n>1),则f(n)
(A)只能被n整除 (B)能被n^2整除 (C)能被n^3整除 (D)能被(n 1)整除 (E)A、B、C、D均不正确
解答:令n=2和3,即可立即发现f(2)=8,f(3)=63,于是知A、C、D均错误,而对于目前五选一的题型,E大多情况下都是为了凑五个选项而来的,所以,一般可以不考虑E,所以,马上就可以得出答案为B。
例:在等差数列{an}中,公差d≠0,且a1、a3、a9成等比数列,则(a1 a3 a9)/(a2 a4 a10)等于
(A)13/16 (B)7/8 (C)11/16 (D)-13/16 (E)A、B、C、D均不正确
解答:取自然数列,则所求为(1 3 9)/(2 4 10),选A。
例:C(1,n) 3C(2,n) 3^2C(3,n) …… 3^(n-1)C(n,n)等于
(A)4^n (B)3*4^n (C)1/3*(4^n-1) (D)4^n/3-1 (E)A、B、C、D均不正确
解答:令n=1,则原式=1,对应下面答案为D。
例:已知abc=1,则a/(ab a 1) b/(bc b 1) c/(ac c 1)等于
(A)1 (B)2 (C)3/2 (D)2/3 (E)A、B、C、D均不正确
解答:令a=b=c=1,得结果为1,故选A。
例:已知A为n阶方阵,A^5=0,E为同阶单位阵,则
(A)|A|>0 (B)|A|<0 (C)|E-A|=0 (D)|E-A|≠0 (E)A、B、C、D均不正确
解答:令A=0(即零矩阵),马上可知A、B、C皆错,故选D。
二、代入法代入法,即从选项入手,代入已知的条件中解题。
例:线性方程组
x1 x2 λx3=4
-x1 λx2 x3=λ^2
x1-x2 2x3=-4
有唯一解
(1)λ≠-1 (2)λ≠4
解答:对含参数的矩阵进行初等行变换难免有些复杂,而且容易出错,如果直接把下面的值代入方程,判断是否满足有唯一解,就要方便得多。答案是选C。
例:不等式5≤|x^2-4|≤x 2成立
(1)|x|>2 (2)x<3
解答:不需要解不等式,而是将条件(1)、(2)中找一个值x=2.5,会马上发现不等式是不成立的,所以选E。
例:行列式
1 0 x 1
0 1 1 x =0
1 x 0 1
x 1 1 0
(1)x=±2 (2)x=0
解答:直接把条件(1)、(2)代入题目,可发现结论均成立,所以选D。
三、反例法找一个反例在推倒题目的结论,这也是经常用到的方法。通常,反例选择一些很常见的数值。
例:A、B为n阶可逆矩阵,它们的逆矩阵分别是A^T、B^T,则有|A B|=0
(1)|A|=-|B| (2)|A|=|B|
解答:对于条件(2),如果A=B=E的话,显然题目的结论是不成立的,这就是一个反例,所以最后的答案,就只需考虑A或E了。
例:等式x^2/a^2 y^2/b^2 z^2/c^2=1成立
(1)a^2 b^2 c^2=x^2 y^2 z^2 (2)x/a y/b z/c=1,且a/x b/y c/z=0
解答:对于条件(1),若a=b=c=x=y=z=1,显然题目的结论是不成立的。所以,最后的答案,就只需要考虑B、C或E了。
四、观察法观察法的意思,就是从题目的条件和选项中直接观察,得出结论或可以排除的选项。
例:设曲线y=y(x)由方程(1-y)/(1 y) ln(y-x)=x所确定,则过点(0,1)的切线方程为
(A)y=2x 1 (B)y=2x-1 (C)y=4x 1 (D)y=4x-1 (E)y=x 2
解答:因切线过点(0,1),将x=0、y=1代入以下方程,即可直接排除B、D和E。
例:不等式(|x-1|-1)/|x-3|>0的解集为
(A)x<0 (B)x<0或x>2 (C)-3<x<0或x>2 (D)x<0或x>2且x≠3 (E)A、B、C、D均不正确
解答:从题目可看出,x不能等于3,所以,选项B、C均不正确,只剩下A和D,再找一个特值代入,即可得D为正确答案。
例:具有以下的性质:(1)它的对称轴平行于y轴,且向上弯;(2)它与x轴所围的面积最小,且通过(0,0),(1,-2)的抛物线为
(A)y=4x^2-6x (B)y=2x^2-3x (C)y=4x^2-3x (D)y=x^2-3x (E)y=x^2-6x
解答:把x=1、y=-2代入选项,即可排除B、C和E。
例:已知曲线方程x^(y^2) lny=1,则过曲线上(1,1)点处的切线方程为
(A)y=x 2 (B)y=2-x (C)y=-2-x (D)y=x-2 (E)A、B、C、D均不正确
解答:将 x=1、y=1代入选项,即可发现B为正确答案。
五、经验法经验法,通常在初等数学的充分条件性判断题中使用,一般的情况是很显然能看出两个条件单独均不充分,而联立起来有可能是答案,这时,答案大多为C。
例:要使大小不等的两数之和为20
(1)小数与大数之比为2:3;
(2)小数与大数各加上10之后的比为9:11
例:改革前某国营企业年人均产值减少40%
(1)年总产值减少25% (2)年员工总数增加25%
例:甲、乙两人合买橘子,能确定每个橘子的价钱为0.4元
(1)甲得橘子23个,乙得橘子17个
(2)甲、乙两人平均出钱买橘子,分橘子后,甲又给乙1.2元
例:买1角和5角的邮票的张数之比为(10a-5b) : (10a b)
(1)买邮票共花a元 (2)5角邮票比1角邮票多买b张
例:某市现有郊区人口28万人
(1)该市现有人口42万人 (2)该市计划一年后城区人口增长0.8%,郊区人口增长1.1%,致使全市人口增长1%
六、图示法用画图的方法解题,对于一些集合和积分题,能起到事半功倍的效果。
例:若P( B )=0.6,P( A B )=0.7,则P(A|B跋)=
(A)0.1 (B)0.3 (C)0.25 (D)0.35 (E)0.1667
解答:画出图,可以很快解出答案为C。
例:A-( B-C )=( A-B )-C
(1)AC=φ (2)C包含于B
解答:同样还是画图,可以知道正确答案为A。
七、蒙猜法这是属于最后没有时间的情况,使用的一种破釜沉舟的方法。可以是在综合运用以上方法的基础上,在排除以外的选项中进行选择。而对于充分条件判断题来说,根据经验,选D和选C的概率比较大一些。
--------------------------
关于备考很多时候选择还是大于努力的,对自己的情况分析到位,备考期间就知道考试期间能够取舍那些地方,这里给大家推荐一个交流群>>679693221<<
,