摘要:灵敏系数是不确定度计算的关键因素,在实际测绘仪器计量检定过程中,输入量的采集方式为不同目标多次测算方式,利用公式计算测量结果,获取输出量。在测量不确定度过程中,基于数学模型的繁杂性,致使对输入、输出量的灵敏系数获取难度加大。文章简要介绍了强行偏导法、方差比例法、传递继承法的计算方法,获取其中的灵敏系数,解决测绘仪器测量不确定度的技术问题。
关键词: 数学模型 测绘仪器 测绘学 测量不确定度 灵敏系数
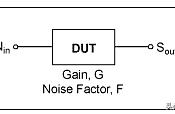
在计量检定程序中,数据报告的结果为:计量检定/校准结果,或者称为测量结果、输出量;输入量并不是直接测量结果,而是依据一定数学逻辑、采取数据处理后,测量分析得出结果。在测绘仪器检定程序中,利用不同目标多次测量输入量,并且利用复杂的数学公式计算所测量数据,计算结果为输出量。输入量与输出量之间存在着不确定度传递关系,所传递的不确定度为“灵敏系数”。
1、灵敏系数在检定经纬仪处于“μ值”时
“μ值”指的是水平方向存在的标准偏差,利用标准角法检定DJ1级经纬仪的灵敏系数。在《光学经纬仪》规定内容中,在使用标准角法检定DJ1级经纬仪“μ值”时,所产生的标准角应采用型号为552的齿多齿分度台;当标准角为零时,让安装在标准角上方位置的经纬仪,与其前方位置的光管保持平行关系;当水平度盘的取值为零时,读数此时的Lo数值;在水平度盘后的多齿台,受检点设定原则为:24齿为一组;采取受检点逆时针旋转j度,j的取值范围为[1,n],n为标准角数量;让经纬仪旋转,采取顺时针旋转方式;经纬仪照准受检点,采取平行光管方式,读取Ly数值;经纬仪往测至360度;将经纬仪设置成倒镜模式,读得Rp数值;转动多齿台,以顺时针旋转方式;经纬仪被检定过程中,以逆时针转动方式;在受检点处进行经纬仪返测,读取R数值;获取多组R数值,直至其为0度;其中测回为:往返测一次,总计历经两个测回。利用下述公式求出灵敏系数。a={(Ly R±180)/2}-{(Ly R-180)/2},(当Ly<180度时,取减号;当L≥180度时,取加号);Ψ=α-β;ψ=Ψ-1/n∑Ψ,∑上方值取n,下方值取j=1;μ={∑1(∑2ψ2)/m(n-1)},其中∑1上方值取n,下方值取i=1,∑2上方值取n,下方值取j=1;μ={∑1(∑2ψ2)/m(n-1)}1/2。
公式中,q代表的是:第i测回第j受检点对零位夹角的测量值;μ代表的是:测回水平方向标准偏差数;L代表的是:第i测回第j受检点盘左侧测量的数值;R代表的是:第i测回第j受检点盘右侧测量的数值;m代表的是:测回次数。由于L、R的取值是在不同时刻、相同环境中,由同一客体对相同装置、不同部位、相同经纬仪、不同受检点,发起的测量,存在重复性精度测量,μ(L)=μ(R)=μ(α),μ2(αi)=1/4μ2(α) 1/4μ2(α) 1/4μ2(α) 1/4μ2(α)=μ2(α),由此可知:受检点标准角的测量,其中的不确定度具有一致性,即μ(βi)=μ(β);最终得出:μ2(μ)=(1/mn)μ2(α) (1/mn)μ2(β);输入量α、标准角β其中的不确定度为输出量μ,计算二者的不确定度灵敏度系数:C(α)={1/mn}1/2=0.147,C(β)={1/mn}1/2=0.147[1]。
2、灵敏度系数在检定全站型电子速测仪“ms”值时
“ms”值代表的是:测距综合标准差时,利用1000米室外基线场,实现检定I级全站型的电子速测仪的灵敏系数。依据《全站型电子速测仪》的具体要求,全站型电子速测仪的ms值,而ms值所需的基线场各段距离L,采用的是用全站型电子速测仪逐段测量方式;基线场各段距离L、基线标准值Doi,比较二者数值,求得加常数K、乘常数R;基线场各段新测量值D的计算方式,是利用K、R数值实现加、乘常数修正,求得结果;基线场各段距离L、基线标准值Doi,二者数值再次比较后,求得测距综合标准差,以此来计算固定误差部分a、比例误差系数b;最终将计算结果划算成1000米测距时产生的综合标准差。
所用公式如下:动态i段基线场距离L=基线标准值Doi-基线场i点距离L;加常数K,是依据基线场距离L、动态i段基线场距离L、n个基线数量之间的数学关系计算得出;乘常数R,与加常数K的算法相似;i段的D值为:Li RLi K=(1 R)Li K;Li取值为基线标准值Doi-Di所得结果的绝对值,即Li=|Doi-Di|;其中Doi所代表的是:第i段基线拥有的标准值;L所代表的是:第i段基线测量实际数值;动态L所代表的是:第i段基线的测量偏差范围;K所代表的是:加常数;R所代表的是:乘常数;n所代表的是基线段数;D所代表的是:第i段基线测量值经加、乘常数修正后,计算得出的数值;Li所代表的是个绝对值,即第i段基线测量新值与该段标准值之差值的绝对值;a所代表的是:测距综合标准差的固定误差范围;b所代表的是:测距综合标准差存在的比例误差系数[2]。由输入量L、D,计算输出量a、b的数学模型,分别展开计算:a=f(L1,L2,Ln,D01,D02,D0n);b=Φ(L1,L2,Ln,D01,D02,D0n);根据公式μc2=∑(σf/σxi)2μ2(xi),考虑Li作为精度测量数值,并且在D0n处数值为最大时,其不确定度值可以代替D0处的不确定度数值;计算过程中,考虑D0n(i=1,2,...3,n)在基线场限定的不确定度,其数值范围随机变化10次,在变化期间其D0值不变;最终求得个输入量、测量数据、标准长度,二者的不确定度,输出量的不确定度,两个不确定度的灵敏系数为:Cmd(L)=0.22,Cmd(D0)=0.22。
3、灵敏度系数在经纬仪装置“Sm”值时
“Sm”值指的是水平角检定装置稳定性,用DJ1级经纬仪检定装置的灵敏系数,并且依据《经纬仪检定装置》规范内容,经纬仪检定装置的水平角检定装置稳定性,其检定方法是:在经纬仪检定装置中,按照《光学经纬仪》检定规范方法,采纳测回水平方向标准偏差的计算方式,利用DJ1级经纬仪,持续检定k次,获得μ(i=1~k);再用以下公式计算测量的灵敏度系数。M={∑μ2/k}1/2,其中∑上方取值为k,下方取值为i=1;Sm=M={∑(μ-M)2/(k-1)}1/2,其中∑上方取值为k,下方取值为i=1;μ代表的是:第i次测量得“测回水平方向标准偏差值”;k代表的是:测量次数(一般情况下,k=6);M代表的是:k次测量数据所得出的几何平均值;Sm所代表的是:水平角检定装置所需的稳定性[3]。
μ值计算需要经过测量诸多方向值α,从中获取计算过程;计算μ到Sm的灵敏系数。μc2=∑(σf/σxi)2μ2(xi);(1)μ2(Sm)=(σSm/σμ1)2μ2(μ1) (σSm/σμ2)2μ2(μ2) ... (σSm/σμk)2μ2(μk);σSm/σμi={1/(k-1)Sm}{(μ1-M)-(μi/Mk)[(μ1-M) (μ2-M) ... (μk-M)]},其中“(μ1-M) (μ2-M) ... (μkM)”是残差的代数和,其计算结果近似等于0,约等于0的极小小数,采取简化计算方式,计算公式为(2):σSm/σμi=(μi-M)/(k-1)Sm;(3):(σSm/σμi)2=(μi-M)2/[(k-1)Sm]2;将(2)、(3)公式代入(1)中,并综合考量任意时间测量经纬仪的“测回水平方向标准偏差值”,其结果具有一致性质的不确定度,即:μ2(μ1)=μ2(μ2)=μ2(μ3)=...μ2(μk)=μ2(μ);因此,μ2(Sm)={∑{(μ1-M)2/[(k-1)Sm]2}}×μ2(μ)={μ2(μ)/[(k-1)Sm]2}∑(μ1-M)2={1/(k-1)}μ2(μ);经过公式计算得出输入量μ,测量数据的不确定度、输出量Sm的不确定度,二者的灵敏系数为:C(μ)={1/(k-1)}1/2=0.45。
4、结论
综上所述,计算灵敏系数的过程中,测绘仪器的测量不确定度被无限缩小,来提升灵敏系数的计算精准度,有利于计量工作的有序运行。测绘仪器具有多重种类、多种项目选择,为分析、处理相关项目提供了诸多便利。尤其在数学模型较为复杂的情况下,利用测绘仪器相关算法,实现计算过程的简单化,例如,电子表格、表格认可等计算。
,