微积分,作为高等数学的重要分支,在物理学研究中有着广泛的应用。它不仅能够描述物体的运动和力的作用,还可以揭示温度变化、热能传递和电场的分布等自然现象背后的数学本质。在物理学的研究中,微积分为我们提供了强有力的数学工具,帮助我们更加深入地理解自然世界。本文将介绍微积分在物理学研究中的应用,为读者带来一次全新的数学与物理学的交叉旅程。
什么是微积分
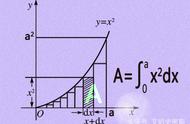
牛顿-莱布尼茨 微积分方程
微积分是高等数学的一个分支,包括微积分学和积分学两部分。微积分学主要研究极限、导数和微分等概念,是一门研究变化的量及其规律的学科;积分学主要研究不定积分、定积分和曲线积分等概念,是一门研究量的累加和面积等问题的学科。
微积分的出现是对几何学和代数学的补充,它为研究物理、力学、天文学、地理学等提供了强有力的数学工具。通过微积分的一系列运算,我们可以更加深入地了解自然界中存在的各种变化规律和机制。
微积分的基础概念包括导数和微分。导数表示一个函数在某一点的变化率,也就是函数值的微小变化量与自变量的微小变化量之比。通常用表示函数 f"(x)的导数。微积分基本定理表明了微积分的导数和积分之间的关系。微分学基本定理则说明了积分的本质:对积分区间内求的所有微小面积进行累加,得到的就是整个区间的面积。
什么是物理
物理学是研究物质的本质、性质和相互作用的学科。它探究自然界中各种现象和规律,并通过物理实验和理论推导来揭示它们背后的科学本质。物理学涉及的范围非常广泛,包括力学、热力学、电磁学、光学、原子物理学、核物理学等多个分支。
物理学不仅是一门基础学科,也是一门应用学科,它在现代生产和科学技术中得到了广泛应用。从能源的探索到科技的创新,从天文学到地理学,都离不开物理学的知识和方法。
微积分在物理学研究中的应用实例3.1 微积分在动力学中的应用
动力学研究物体的运动与力之间的关系,它包括牛顿力学和万有引力定律等理论。微积分在动力学中的应用,主要用于描述力和物体运动之间的关系。通过牛顿第二定律 F=ma和万有引力定律等公式中的微积分,可以计算物体的加速度和受到的力。
例如,我们可以使用微积分来解决下面这个经典的力学问题:一个质点以初速度 垂直于水平面飞行,受到一个竖直向下的重力 mg 和一个阻力 的作用。求出质点的轨迹。根据牛顿第二定律,质点的运动状态满足: