思维立足于思想,思想衍生出方法.数学思想方法如今成为了数学"四基"之一,也是数学新课标要求之一.在现行初中数学教科书中,蕴藏着很多的数学思想方法,值得挖掘.立足课本是先手.用好现行数学教科书上的思想方法是一门高深的学问,在前面发布文章中或多或少有些叙述. 事实上,还有不少书上没有提及到的数学方法在平常数学课堂教学中也可以插入学习,特别是与高中数学衔接的一些数学方法更有必要掌握下来,在平时解题一些"提升拓展题"或"压轴题"等可以活用、巧用、捷用.

1.探究活动一:

探究活动二
数学兴趣小组继续深入研究直线的"斜率"问题,得到正确结论:任意两条不和坐标轴平行的直线互相要直时,这两条直线的斜率之积是定值.
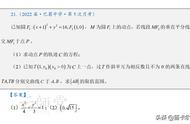
如图2,直线DE与直线DF垂直于点D,D(2,2),E(1,4),F(4,3).请求出直线DE与直线DF的斜率之积.
综合应用
如图3,⊙M为以点M为圆心,MN的长为半径的圆,M(1,2),N(4,5),请结合探究活动二的结论,求出过点N的⊙M的切线的解析式.

∵直线PQ经过点N(4,5),∴5=﹣1×4 b,解得 b=9,
∴直线PQ的解析式为y=﹣x 9.
本题主要考查了圆的切线性质,待定系数法求一次函数解析式,新定义:直线斜率;是一道创新题,引入新定义:直线斜率,理解和掌握直线斜率的概念是解题的关键.
遇上平面直角坐标系的考题,欲证明某一个三角形是直角三角形,可以考虑使用"斜率互为负倒数的两直线垂直k₁•k₂=﹣1."这个神奇的结论,可以快速破解直角三角形存在性问题。