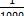又比如在财务会计记账的时候,通常是以元为单位,角、分用小数表示,且分不删去。例如10元1角记作10.10元,切不可把末位0去掉记作10.1元。0.10也不能记成0.1。

在超模君的训练下,8岁表妹已经有科研精神的苗头了,抛出了个问题:精确小数简简单单多好呀,为什么要提出近似小数呀?
为什么要有近似小数?
其实,在实际问题中许多数值是无法完全准确的,许多数值要求不必弄得完全准确的,只考虑这些数值的大概的数值。
比如别人问你多大了?你说8岁,这就是一个近似值,如果要精确就变得很麻烦,你要讲8岁零几个月,8岁几个月又几天,8岁几个月有几天零几个小时几分......
没有近似小数,报个年龄都得花几分钟,要思考要计算,还不一定报得准!

不同事情要求的精确程度也不一样!像报年龄,我们一般只需近似到年就行了。但是在原子物理学中“超子”的寿命只有10^-10到10^-8秒,非常短暂,要弄清它们的年龄起码要近似到10^-10到10^-8秒。
回到数学的问题上。在数学上,存在着小数点后面有着数不尽数字的数,如果没有近似小数,那这些数就很难运用起来了。
在这里,必须提名神奇的圆周率π,这个有着几千年历史的数。π小数点后面的数到现在还没有计算完,或者说永远都计算不完,2019年3月14日,谷歌宣布圆周率现已到小数点后31.4万亿位。

圆周率的地位不用多讲,毕竟每年3月14号这一天都是属于它的。这个无穷无尽的数在我们的科学研究或者生活中几乎是不可或缺的存在!
- 比如我们在计算一块形状为圆的地的面积时,只能把π近似为3.14,得到一个确切的数,才能清晰明了;
- 微积分、高等三角恒等式,是由研究圆周率的推动,从而发展出来的。π对于数学的发展起着非常重要的推动作用。
- 通过计算π还可以测验计算机有没有问题,包括软件和硬件上的问题,没想到吧。
8岁的表妹又问了,可是,怎么会有存在这么无理的数?
无理数的数学危机
哎,还真就的就是无理数!
无理数是一个充满了血腥的数。我们都知道,说真话的人常常会被针对,特别是说真话会触犯到他人利益的时候。
在公元前500年,古希腊大数学家毕达哥拉斯提出“万物皆为数”的观点:数的元素就是万物的元素,世界是由数组成的,世界上的一切没有不可以用数来表示的,数本身就是世界的秩序。