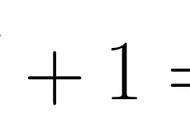探究2重复运用了探究1的递推公式的特例。其中除了求和公式,还有求积公式,总结起来非常麻烦,烧脑。它的原理是通过对正弦降幂,一直降到零次幂,就可以得到关于e^x的不定积分的式子,问题自然就解决了。
上图仅探究了n是偶数的情况。先看一道这方面的例2:求∫e^x*(sinx)^6dx.

那么当n是奇数时,又会怎么样呢?当n是偶数时,通过降幂,可以将正弦的指数降为0,当n是奇数时,只能降到1次幂,如下图:

因此,我们可以特别地给I1求出来,即求出当n=1时的不定积分公式。如下图:

这样就可以得到n是奇数时的公式,如下图: