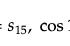一女生:sinA.
师:好!好!(教师连连称赞)那么,菱形ABCD面积又是多少?
生:(全体齐声)9sinA.
师:(乘势深入)好!如果把边长为3一个内角为α的菱形面积记为s,s为多少?
生:(似乎找到了初步的规律,兴奋地)
s= 9sinα. (1)
师:太好了!请同学们写出表达式
生:(学生回答教师板书)S(菱形)=9sinα.
师:对!这样我们可以得出什么结论呢?(学生边回答,教师边板书:设边长为a的正方形面积为S,边长为a、一个内角为α的菱形面积为s,那么s/S=sinα).
师:(引申)那么,这个结论对长方形是不是成立呢?如图5,一个一边长为3,另一边长为5的长方形图形的面积S为多少?若将角A变成α度,则所得菱形(图6)的面积s又是多少呢?

图5

图6
生:(很快)
S(长方形)=15;s(菱形)=15sinα. (2)
帅:(赞许地)好!这样找们就可以得出这样一个维结论:设边长分别为a和b的长方形面积为S,边长为a和b、一个内角为α的平行四边形面积为s,那么s/S=sinα,其中,S是边长分别为a和b的长方形面积。
......
通过上面的讨论,学生对正弦的概念开始有了一个初步的认识,在这个过程中,“面积”概念的过渡性引入使正弦这个抽象的数学符号有了直观的模型。
【片段二:正弦再理解】
正弦的概念引入后,教师稍作巩固,并以此构建理解的第一个台阶,就开始了从特殊值到一般值的教学推进,希望能与学生一起寻找并发现帮助全面理解并掌握正弦涵义的桥梁。
师:我们继续研究边长为1的正方形(图1)。通过刚才的讨论,我们已经知道当角A发生变化时(图2),面积就会发生改变,而且这个改变可以用sinα表示,为了进一步理解sinα,我们先来打个比方,比如买一件商品,原来价格100元,现在打折,只要80元就够了,问这件商品打了几折?
生:打8折。
师:对!再回到刚才对sinα的讨论。大家看,当角A为a时,我们可以用sinα表示它的面积。具体地说,当α=30°时, sinα=1/2,S(菱形)=1/2。我们是否可以认为菱形面积是正方形的面积打了5折后得到的?在这里sin30°相当于一个折扣。
生:(没有马上回答,似乎在思索着什么)……
师:大家再用计算器来计算一下,当α=60°时,菱形的面积是多少呢?
生:0.866.
师:对!因此,我们是不是同样可以认为:一个边长为1,一个角α=60°的菱形面积是由单位正方形的面积约打了八六折得到的?就是:s(菱形)=sin60°=0.866.
生:(似有所悟)可以这样说。
师:(乘势引导)也就是说,在一般情形下,当角A为α时,菱形的面积S(菱形)=sinα可以怎样理解?
生:折扣是sinα!
师:(继续引导)好!我们再来看边长为a=3的正方形,如图3和4,当角A为α时面积的折扣是多少?原来面积是9,现在面积应该是多少?
生:折扣是sinα,现在面积是9sina!
师:对!在这种情形下,sinα还是一个折扣。当α=30°时,菱形面积=9sin30°。面积打五折了,同样当α=60°时,面积就约打八六折。根据上面的讨论结果,我们是不是可以这样认为:平行四边形的面积就是长方形面积打sinα折后得到的?
生:对!
师:我们是不是可以进一步认为,无论是单位正方形、一般正方形,还是长方形,只要它的一个角改变成α,它的面积就打折扣了,这个折扣就是sinα.
生:(略作思考,齐声)对!
至此,学生对正弦的概念有了一个较为完整的理解。在这个过程中,如果说“面积”这个过渡性的概念的引入使学生对“正弦”概念有了空间意义上的认识,那么,另一个过渡性概念“折扣”则使学生开始有了代数意义的初步思考。
二、“菱形面积定义正弦”教学效果的形成性检验为了检验教学效果,我们在教学过程中穿插安排了教学效果的形成性检验。
(一)教师引导下的练习。检验方法:例题分析;检验目的,①巩固已学概念;②适当引申,并归纳出正弦性质;③为后续学习做好铺垫。
【片段三:探究正弦性质】
【例】一个边长分别为a和b的 长方形ABCD(图7),改变角B,使它成为一个内角为B=α的平行四边形ABCD,那么平行四边形ABCD的 面积是多少?

师:哪位同学能回答?
生:(争先恐后)长方形ABCD面积ab打一个sinα折扣。 S(平行四边形)=absinα.
师:好!两边分别为a和b夹角为α的三角形面积是多少?(图8)