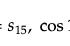生:(很多学生齐声)BC
师:(继续追问)长方形ABCD面积为多少?
生:BA×AC.
师:那么平行四边形ABED面积是多少呢?
生:BC×AD.
师:(继续分析)我们知道从长方形(图9)变为平行四边形(图10),面积打的折扣就是sinA。而平行四边形的面积为底乘高,当长方形ABCD的角A发生变化,长方形(图9)变为平行四边形(图10)时,它的底有没有变化?
生:(齐声)没有!
师:那么到底是谁打了折扣呢?
生:高!
师:对!就是这个高打了折扣,所以面积变化是由高的变化所引起的,其实就是高打了sinA折,即BC=BA×sinA.
师:(继续启发)根据小学学过的折扣的知识,BC是由BA打sinA折得到,那么sinA又可以怎样表示?
生:sinA=BC/BA.
师:(指着图10)同学们,在直角ΔABC中看,角A的正弦与边的关系是……?
生:sinA是角A的对边与斜边的比。
然后,教师又让学生拿出含有30°角的三角板,通过度量30°角所对的直角边与斜边长度,验证
sin30°=对边/斜边=1/2

于是师生共同得出结论四:在直角三角形ABC中,一个锐角A的正弦等于这个角的对边与斜边之比。
【练习二】
1. 如图1,ΔABC中∠C=90°,BC=6,sinA=0.6,求AB的长。

2. 在第1题中如果AC=8,求sinB.
3. 比较大小
(1)sin30° _______ sin80°
(2)sin100° _______sin140°
4.两块同样的三角板如图2放置,则黑色部分的面积是否相等?为什么?

从练习二的情况看,多数学生对前3个练习解答都比较顺利,对第4小题,尽管有个别同学能够写出答案,不少同学仍感到困难。但他们在教师的启发、引导下,大多数学生还是很快弄明白,课堂练习顺利完成。
(三)课后了解。目的:了解学生学习兴趣。进一步巩固学习的信心。
下课后,我就近问旁边的同学“正弦是什么?”几个学生抢着说“正弦就是打折”,我又问“今天老师讲的内容能听懂吗?”他们一起回答说“懂”。
三、教学反思
分析“重建三角”的教学过程,结合穿插在教学过程中形成性检验的结果分析,我们可以得出:
1. 用直观的“面积”、“折扣”引入较为抽象的“正弦"概念,能降低教学台阶,学生掌握新概念比较顺利。而且由于抽象概念的形象描述,克服了以往正弦概念教学中从抽象到抽象的弊端。
2. 以“面积”、“折扣”为过渡性概念作铺垫,教学引申比较顺利,变式训练的难度大大降低。学生在学习过程中始终保持浓厚的 兴趣,对后续学习产生了强烈的期待,学习的动力被进一步激发。
3. 从数学思维的培养角度分析,“面积”的引入拓展了学生对正弦概念的“形”的思考,而“折扣”的引入又启动了学生的“数”的思维。这种全新的课程逻辑体系将有利于学生“数、形”融合,使后续学习的思维空间得到整体的拓展,防止数学整体思维的人为割裂。
综上所述,“面积”和“折扣”并不是本节课教学的目标性概念,而是一个有用的、为引入和理解正弦涵义的形象的过渡性概念。"面积”、“折扣”的引入不但有利于降低学习的台阶、降低教学的难度,更为重要的是,通过这两个过渡性概念的引入,在三角、几何、代数间搭建了一个互相联系的思维通道。我们希望,这一尝试能为“重建三角"的教学探索提供一个教学案例。
作者:
(宁波教育学院 崔雪芳)
参考文献
张景中.2006.重建三角,全盘皆活——初中数学课程结构性改革的的一个建议.数学教学,(10):封二~4
张奠宙.2006.让我们来重新认识三角——兼谈数学教育要在数学上下功夫.数学教学,(10):5~10