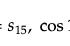生:(一下子没有回答).
师:我们一起讨论,在图7中连接AC,就把平行四边形 ABCD分成两个三角形,那么三角形ABC的面积是平行四边形ABCD面积的……
生:(似乎豁然开朗,半数左右学生齐声)一半!
师:好!(板书):
S(△ABC)=1/2absinα.

师:(出示图1和2)当A角为0°,180°,90°时,它们的面积各为多少?
生:(讨论)它们的面积分别为0,0,1.
师:我们把这个结论写在黑板上(板书):
(1)sin0°=sin180°=0;
(2)sin90°=1;
(3)sinα=sin(180°-α);
(4)当α为锐角时,α越大sinα就越大。
从例题解决的情形看,学生们已经很好地掌握了通过“面积”、“折扣”引出的正弦概念,而且,通过面积、折扣容易地得出了正弦的基本性质,尤为重要的是,公式
S(△ABC)=1/2absinα

的得出,为三角、几何和代数后续学习做好了重要的铺垫。
(二)课堂练习检验。检验方式:学生独立完成课堂练习,教师针对性分析。目的:①进一步巩固;②发现知识掌握的不足;③为整体理解找帮助。
【练习一】
1. 用计算器求值
(1)sin30°,(2)sin45°,(3)sin60°,(4)sin120°
2. 边长分别为2和4,一个内角为30°的平行四边形ABCD的面积是_______.
3. 两边分别为6和5,夹角为45°的三角形面积是_______.
4.在括号内写出和左端不同的角的度数,使等式成立。
sin40°=sin( ) ,sin170°=sin( ).
绝大多数学生都在几分钟内顺利完成,而且回答得很准确。
在检查了学生课堂练习后,教师乘势作了新的引申:
【片段四:正弦再认识】
师:请同学们继续研究平行四边形的面积(图9),点B到 AC的距离是多少?

生:线段BA.
师:对,那么在图10中,点B到AD的距离是多少呢?