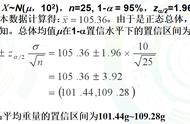设总体的分布函数含有一个未知参数 θ,θ∈Θ(Θ 是 θ 可能的取值范围);对于给定值 α(0<α<1),若由来自 X 的样本确定的两个统计量 和
对于任意 θ∈Θ 满足:
则称随机区间是 θ 的置信水平为 1−α 的置信区间。其中,为置信下限,为置信上限,1−α 为置信水平。
固定样本容量 n,若反复抽样多次,每个样本值确定一个区间,每个这样的区间要么包含 θ 的真值,要么不包含 θ 的真值。
按大数定律,在这么多区间中,包含真值的约占 100∗(1−α)%,不包含真值的占 100∗α%。

置信水平为 1−α 的置信区间并不是唯一的。对于正态分布这种单峰且对称的情况,对称的区间长度最短,意味着估计的精度最高。

置信区间与样本容量的关系:

- 标准误随着样本容量的增加而减小
- 误差范围随着样本容量的增加而减小
设总体, 已知,μ 未知,设是来自 X 的样本,求 μ 的置信水平为 1−α 的置信区间。

解读:
- 现在得到的区间属于那些包含 μ 的区间的可信程度为 100∗(1−α)%
- 或者说“该区间包含真值”这一陈述的可信程度为 100∗(1−α)%