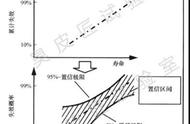
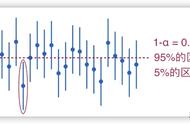
这里也没有狄拉克三角洲,所以与我的主观实验不同,它的可信区间是一维的。
消除p=0然而,情况与我们的直觉相反。
在生命中的每一天都购买彩票直到80岁生日去世的新生儿有99.99%的机会永远不会持有中奖彩票。

用数百万年来降低置信区间或可信区间的彩票10%的容错率
p=0当您的时间有限时,这始终是一选择。这新实验的问题在于它非常强大。如果我们的口袋里没有真正的获胜几率,我们可能会被指责为把我们的拇指放在天平上。
我们可以淡化(1,299999999)将两者分开α和β由异常数值。这保持了Beta分布的均值,而p=0案例现在具有非零可信度我已经证明这没什么大不了的。
选择适当的常量值,我们得到类似(ε,1),在那里ε是一小的正值。毫不夸张地说,这是在我一直在炒作的主观之前的epsilon之内!
目标不是找到获胜概率小于0.1目标是找到获胜概率p在小于0.1*p的误差范围内。
因此,如果p=1.0/300e6~3.3e-9并且您希望答案在3.3e-10以内,您将需要采集很多样本。

用数百万年来降低置信区间或可信区间的彩票10%的容错率
想要一置信区间或可信区间,使得在区间为[p–0.1p,p 0.1p],其中p是平均值的间隔?我问是因为贝叶斯统计和常客统计都没有承诺置信区间/可信区间包含真正的价值,所以简单地阅读你的解释是没有意义的。
或多或少是的,无论您考虑2sigma还是1sigma或其他不重要的东西,间隔是否以实际真实值为中心也不重要。
重要的是,他正在寻找一区间,其比例约为真值的10%*。*当真值很小时,区间也很小。
这就是他所说的“相对”与你的计算相比的意思,你的计算是“绝对”大小小于0.1。
就涉及相对与绝对误差而言,3.3e-9真值的10%表示误差宽度为3.3e-10。

用数百万年来降低置信区间或可信区间的彩票10%的容错率
我们如何知道何时停止采样?如果我们知道我们的目标错误宽度是3.3e-10,那么我们就知道获胜的几率是3.3e-9,如果我们知道获胜的几率,我们就根本不需要任何样本。
相反,这种解释如何:当置信区间的形式为[0.9*x,1.1*x]时,对于x的某实数值,我们停止采样。现在我们根本不需要知道真正的价值。
当然,或者如果sd是平均值的0.1倍,无论您使用什么作为标准,如果它导致采样直到您确定该值在10%以内并且该值是一很小的数字,那么您将采取大量的样本。
这是因为对于小p,stddev就像sqrt(p*(1-p)/N)=0.1p,我们假设p很小,我们可以忽略p^2并得到sqrt(p/N)~0.1p,两边平方,p/N~.001p^2,N~100/p,如果p在1/300M的量级那么N在300亿的量级。

用数百万年来降低置信区间或可信区间的彩票10%的容错率
已经解决了这问题的贝叶斯方面,关键的不平等是(sigma)/(A b n)*sqrt(A*(b n)/(A b n 2))>Aandn>>b,并在这些假设下整理数学。现在你得到
(sigma/T)^2<=A=a w,
其中“w”是彩票中奖次数。这与您的常客版本一致:如果我们先采用(1,1)Bayes/Laplace,如果sigma=1,我们需要中奖99次,如果sigma=2,我们需要中奖399次。
我们不关心n的值,只要它淹没了实验。如果我们假设s非常大,我们也可以从第一种方法中得出这结果。

用数百万年来降低置信区间或可信区间的彩票10%的容错率
还有第三种消除不等式的方法,即断言A=0。这会将其转换为0<=0,这是正确的,因此我的主观(0,1)实验不需要单样本。频率统计需要“合理的”n,但对于我们使用的典型样本量,在绝大多数情况下,它仍然会导致最大似然为0和置信区间为0。
这符合您的参数以及内曼对频率论置信区间的要求,因此我们可以在远低于“数百万年”的时间内得出结论。
频率论仍然以两相互矛盾的答案结束。与贝叶斯统计不同,它不能将责任归咎于实验的选择,因此这是一合法的悖论。

用数百万年来降低置信区间或可信区间的彩票10%的容错率
,