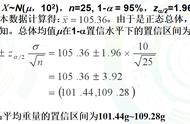置信水平转换方案,置信水平通俗理解

今晚重温下数据统计，学习以下内容：

1、对给定数据进行探索性数据分析。

2、计算描述性统计数据并绘制直方图。

3、使用 scipy 库计算置信区间、Z-score和 T-score。

置信区间(confidence interval)：即误差范围。

用（a, b）表示，a和b的确切数值取决于事件对于“该区间包含总体均值”这一结果的可信程度。

置信区间在频率学派中间使用，其在贝叶斯统计中的对应概念是可信区间（credible interval）

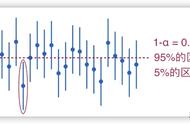
从正态分布产生的50个样本中得出的50个置信区间

置信水平(Confidence level)：即置信区间包含总体平均值的概率多大。

例如，95%的置信水平指的是100个置信区间有95个包含了总体平均值。置信水平越高，区间越宽，置信区间包含总体统计量的几率越大，但置信区间太宽，则会失去意义。常用置信水平为95%。

我们常犯一个概念性错误，是将基于观测到的数据所同样构造的置信区间的置信水平，误认为是它包含真实未知参数的真实值的概率。正确的理解是：置信水平只有在描述这个同样构造置信区间的过程（或称方法）的意义下才能被视为一个概率。

Z分数：

z分数（z-score），也叫标准分数（standard score）是一个数与平均数的差再除以标准差的过程。在统计学中，标准分数是一个观测或数据点的值高于被观测值或测量值的平均值的标准偏差的符号数。

z分数可以回答这样一个问题："一个给定分数距离平均数多少个标准差?"在平均数之上的分数会得到一个正的标准分数，在平均数之下的分数会得到一个负的标准分数。z分数是一种可以看出某分数在分布中相对位置的方法。

T分数：

T分数是原始分数的导出分数。把原始分数转换成标准化分数为线性转换，Z分数与原始分数的分布形状相同，原始分数为正态分布，则Z分数也为正态分布。

原始分数如果不是正态分布，如何使导出分数为正态分布呢?这时可先把原始分数转换成百分等级，而后再把百分等级转换成标准正态分布的z值，从而迫使导出分数z服从均数为0、标准差为1的正态分布，叫做正态化的标准分数。

import pandas as pd import numpy as np import matplotlib.pyplot as plt import seaborn as sns df = pd.read_csv('Q7.csv') df.head()

输出：

df.describe()

输出：

df['Weigh'].mode()

输出：

0 17.02 1 18.90 Name: Weigh, dtype: float64

df['Weigh'].var()

输出：

3.193166129032258

df['Weigh'].std()

输出：

1.7869432360968431

df['Weigh'].max() - df['Weigh'].min()

输出：

8.399999999999999

sns.boxplot(df)

输出：

sns.scatterplot(df)

输出：