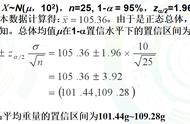置信区间是统计学中一个重要的概念,它提供了一个参数的可能范围,以及这个范围的置信度。这个参数可能是总体的均值、比例、差异或其他统计量。在实际研究中,由于我们通常不能获取到所有的总体数据,因此我们需要通过抽样来估计总体参数。置信区间就是这种估计的一个重要工具。
**基本概念**
首先,让我们来理解一下置信区间的基本概念。假设我们对一个总体进行了随机抽样,然后计算了样本的均值和标准差。由于抽样误差的存在,样本均值可能会略微偏离总体均值。我们可以使用样本均值和样本标准差来估计一个范围,我们认为这个范围内有一定的概率包含总体均值。这个范围就是置信区间,而这个概率就是置信水平。
**置信水平和置信区间**
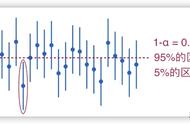
置信水平通常用百分数表示,比如95%,99%等。一个95%的置信区间意味着,如果我们无限次地从总体中进行抽样,并对每个样本计算95%的置信区间,那么这些置信区间中大约有95%会包含总体的真实参数。
需要注意的是,置信水平并不意味着特定的置信区间有多少概率包含总体参数。例如,对于一个给定的95%置信区间,我们不能说这个区间有95%的概率包含总体参数。这是因为总体参数是固定的,不涉及概率。置信水平是对我们的方法的信任度,而不是对特定区间的信任度。
**计算置信区间**
在实际中,置信区间的计算通常基于特定的统计分布,比如t分布或者正态分布。例如,对于总体均值的估计,我们通常会使用以下公式来计算置信区间:
样本均值 ± t值 × (样本标准差/√样本大小)
其中,t值取决于所选择的置信水平和样本大小。样本标准差/√样本大小被称为标准误差,它是样本均值的标准偏差,反映了样本均值的变异性。
**解释置信区间**
在解释置信区间时,我们需要注意以下几点:
1. 置信区间是对总体参数的一种估计,它提供了一个可能的范围,而不是一个确切的值。
2.
2. 置信区间的宽度反映了估计的准确性。较宽的置信区间说明估计的不确定性较大,这可能是由于样本大小较小、样本变异性较大或置信水平较高等原因造成的。相反,较窄的置信区间说明估计的不确定性较小。
3. 虽然置信区间提供了一个可能的范围,但我们不能说总体参数有多少概率落在这个范围内。总体参数是一个固定的值,不涉及概率。置信水平是对我们的方法的信任度,而不是对特定区间的信任度。
4. 置信区间是对抽样误差的一种量化。抽样误差是由于我们只能观察到总体的一部分(即样本)而产生的。通过计算置信区间,我们可以了解抽样误差可能导致的误差范围。
**置信区间的应用**
置信区间在各种研究中都有广泛的应用。例如,它们可以用于估计总体的均值、比例或差异,也可以用于做出统计推断,比如假设检验。在假设检验中,我们可以通过看总体参数是否落在置信区间内,来决定是否拒绝零假设。
此外,置信区间也常常用于表达研究结果的不确定性。例如,一个研究报告可能会说:“我们95%的置信区间是[5, 10],这意味着我们有95%的信心,总体均值在这个范围内。”
总的来说,置信区间是一种重要的统计工具,它帮助我们理解和量化抽样误差,使我们能够对总体参数进行更准确和可靠的估计。
,