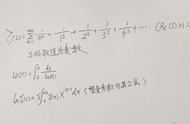向量点乘和叉乘的区别:向量点乘结果是标量,是两个向量在一个方向的累计结果,结果只保留大小属性,抹去方向属性,就相等于降维;向量叉乘,是这这两个向量平面上,垂直生成新的向量,大小是两个向量构成四边形的面积。相等于生维。这是运算所需要,向量加和减都是在同一纬空间操作的,如果要想实现维度的变化就要在向量的乘法做出定义。
向量点乘(内积):
点乘(Dot Product)的结果是点积,又称数量积或标量积(Scalar Product),结果就是个数,把方向给抹去了。向量是有两个属性的:大小和方向,点乘的结果就是得到一个标量。相等于降维了。

定义为:对两个向量对应位置上的值相乘再相加的操作,其结果即为点积。

从这个结果来看,就知道没有方向属性,只是数字之间的运行,最终结果也是数字。
从几何角度看,点积是两个向量的长度与它们夹角余弦的积。点乘的结果表示向量A在向量B方向上的投影与向量B模的的乘积,点乘的意义就是两个向量在一个向量方向的共同积累的结果,但是这种结果只保留的大小属性,抹去了方向这个属性;同时反映了两个向量在方向上的相似度,结果越大越相似。基于结果可以判断这两个向量是否是同一方向,是否正交垂直,具体对应关系为:
.则方向基本相同,夹角在0°到90°之间
.则正交,相互垂直
.则方向基本相反,夹角在90°到180°之间