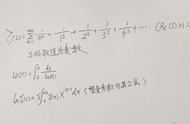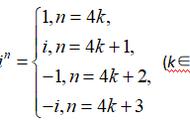向量的加法运算
,
学习目标
1.理解并掌握向量加法的概念.
2.掌握向量加法的三角形法则和平行四边形法则,并能熟练地运用这两个法则作两个向量的加法运算.
3.了解向量加法的交换律和结合律,并能作图解释向量加法运算律的合理性.
一、向量加法的定义及三角形法则
知识梳理
1.向量加法的定义
求两个向量________的运算叫作向量的加法.
任一向量与其相反向量的和是__________.
2.向量求和的三角形法则
向量求和的法则 | 三角形法则 | 已知向量和,在平面内任取一点O,作=,=,则向量______叫作与的和,记作________,即+=+=________. 根据向量加法的定义得出的求向量和的方法,称为向量加法的________法则 |
1.向量加法的运算律
(加法交换律)+=+;
(加法结合律)(++c=+(+c).
2.向量加法的平行四边形法则
向量求和的法则 | 平行四边形法则 | 对于任意两个不共线的非零向量,,分别作=,=,以OA,OC为邻边作▱OABC,则以O为起点的对角线表示的向量就是向量与的和.这种求两个向量和的方法叫作向量加法的________________法则 |
(2)向量加法的平行四边形法则和三角形法则的区别和联系
区别 | 联系 | |
三角形法则 | ①首尾相接 ②适用于任何两个非零向量求和 | 当两个向量不共线时,三角形法则作出的图形是平行四边形法则作出图形的一半 |
平行四边形法则 | ①共起点 ②仅适用于不共线的两个向量求和 |