甘肃2023统招专升本考试内容整理—制图基本知识关于平面的投影,考点整理如下,希望对大家有所帮助。
(一)平面的表示法
在投影图上表示平面有两种方法。
1、一组几何元素的投影表示平面
(1)不在同一直线上的三点
(2)一直线和直线外一点
(3)相交两直线
(4)平行两直线
(5)任意平面图形,如三角形、四边形、圆形等
(二)平面对于一个投影面的投影特性
空间平面相对于一个投影面的位置有平行、垂直、倾斜三种,三种位置有不同的投影特性。
1、真实性 当平面与投影面平行时,则平面的投影为实形。
2、积聚性 当平面与投影面垂直时,则平面的投影积聚成一条直线。
3、类似性 当直线或平面与投影面倾斜时,则平面的投影是小于平面实形的类似形。
(三)各种位置平面的投影特性
根据平面在三投影面体系中的位置可分为投影面倾斜面、投影面平行面、投影面垂直面三类。前一类平面称为一般位置平面,后两类平面称为特殊位置平面。
1、投影面垂直面
垂直于一个投影面且同时倾斜于另外两个投影面的平面称为投影面垂直面。垂直于V面的称为正垂面;垂直于H面的称为铅垂面;垂直于W面的称为侧垂面。平面与投影面所夹的角度称为平面对投影面的倾角。α、β、γ分别表示平面对H面、V面、W面的倾角。
举例说明:铅垂面的投影特性

铅垂面
强调:(1)两个投影均为类似形;
(2)一个投影积聚为直线,并反映β、γ角。
总结投影面平行线的投影特性:两面一线。
对于投影面垂直面的辨认:如果空间平面在某一投影面上的投影积聚为一条与投影轴倾斜的直线,则此平面垂直于该投影面。
2、投影面平行面
平行于一个投影面且同时垂直于另外两个投影面的平面称为投影面平行面。平行于V面的称为正平面;平行于H面的称为水平面;平行于W面的称为侧平面;
举例说明:正平面的投影特性

正平面
强调:(1)两个投影积聚为直线;
(2)一个投影反映实形。
总结投影面平行线的投影特性:两线一面。
3、一般位置平面
与三个投影面都处于倾斜位置的平面称为一般位置平面。

一般位置平面
例如平面△ABC与H、V、W面都处于倾斜位置,倾角分别为α、β、γ。
一般位置平面的投影特征可归纳为:一般位置平面的三面投影,既不反映实形,也无积聚性,而都为类似形。
(一)平面上的直线和点
1、平面上的点
点在平面上的几何条件是:点在平面内的一直线上,则该点必在平面上。因此在平面上取点,必须先在平面上取一直线,然后再在该直线上取点。这是在平面的投影图上确定点所在位置的依据。
2、平面上的直线
直线在平面上的几何条件是:
(1)若一直线通过平面上的两个点,则此直线必定在该平面上。
(2)若一直线通过平面上的一点并平行于平面上的另一直线,则此直线必定在该平面上。
属于平面且又平行于一个投影面的直线称为平面上的投影面平行线。平面上的投影面平行线一方面要符合平行线的投影特性,另一方面又要符合直线在平面上的条件。
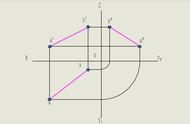
2、举例:如图2-46所示,过A点在平面内要作一水平线AD,可过a′ 作a′ d′ ∥OX轴,再求出它的水平投影ad,a′ d′ 和ad即为△ABC上一水平线AD的两面投影。如过C点在平面内要作一正平线CE,可过c作c e∥OX轴,再求出它的正面投影c′ e′,c′ e′ 和ce即为△ABC上一正平线CE的两面投影。

平面内做直线
,