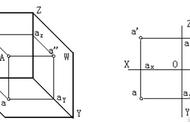
因此可以得出平面方程的通式:
ax by cz d = 0, 其中 d = −ax0 − by0 − cz0
一般系数用大写字母则有平面方程:
Ax By Cz D = 0
点到平面的距离
有了上面的预备知识,我们就可以求点到平面的距离。

上图P点到平面的距离d就是向量RP的长度,而RP在n上的投影长度就是点P到平面的距离。
利用v在u上的投影公式:

由此得出点到平面的距离以矢量的表达方式为:

上面的公式中的Q点是平面上的任意一点,对于平面外的任意一点P来说,我们只有知道QP的向量即可,令Q是(0,0,0), 那么QP=< x, y, z >
根据我们前面谈到的平面方程为Ax By Cz D = 0,显而易见n=<A,B, C >是该平面的一个法线矢量,带入上面的公式就有点到平面的坐标表达式: