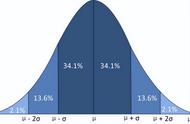
正态分布(也称为高斯分布)是统计学中一种常见的连续概率分布,其概率密度函数可以用来描述许多自然现象,例如测量误差、人口身高、测试成绩等。正态分布的概率密度函数可以用以下公式表示:
\[ f(x) = \frac{1}{\sigma \sqrt{2\pi}} e^{ -\frac{(x-\mu)^2}{2\sigma^2}} \]
其中,\( \mu \) 是均值,\( \sigma \) 是标准差。在正态分布中,均值决定了分布的中心位置,标准差决定了分布的宽度。
假设我们有一个均值 \( \mu = 10 \),标准差 \( \sigma = 2 \) 的正态分布。我们可以使用上述概率密度函数来计算在特定取值处的概率密度值。例如,我们想要计算在 \( x = 12 \) 处的概率密度值,我们可以将 \( \mu = 10 \)、\( \sigma = 2 \)、\( x = 12 \) 代入上述公式中进行计算。
\[ f(12) = \frac{1}{2 \sqrt{2\pi}} e^{ -\frac{(12-10)^2}{2*2^2}} \]
通过计算,我们可以得到在 \( x = 12 \) 处的概率密度值。这个值表示了在正态分布中取到 \( x = 12 \) 的概率密度,可以用来衡量随机变量落在该点附近的概率大小。
,