正态分布是统计学知识,但在生活中最常用得到,学的时候可能不理解,但应用起来却很容易。
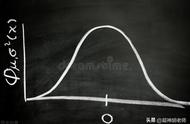
先看这个图,是不是觉得很熟悉?很多统计数据的分析都用得到这张图,比如测量的误差、人体的身高、学生考试成绩等等。数学上称之为“服从正态分布”。

图1 正态分布图
图中表明正态分布的核心是概率区间。正态分布的主要参数有两个:
(1)μ:数学期望或均值,是最有可能出现的结果。
(2)σ2:方差,数据的分散程度。
正态分布和两个参数μ和σ^2强相关,是连续型随机变量的分布,第一参数μ是服从正态分布的随机变量的均值,第二个参数σ^2是此随机变量的方差,所以正态分布记作N(μ,σ2)。
μ是正态分布的位置参数,描述正态分布的集中趋势位置。概率规律为取与μ邻近的值的概率大,而取离μ越远的值的概率越小。正态分布以X=μ为对称轴,左右完全对称。正态分布的期望、均数、中位数、众数相同,均等于μ。
σ描述正态分布资料数据分布的离散程度,σ越大,数据分布越分散,σ越小,数据分布越集中。也称为是正态分布的形状参数,σ越大,曲线越扁平,反之,σ越小,曲线越瘦高。
说到这里,出一道数学题,已知某地统计成绩的前30%区间为7**以上,前45%区间为7**以上,通过正态分布就可计算出前8%区间是***以上,甚至可以算出来800以上所占生源比例。
数学是理智科学,有空的可以来算算也来聊聊科学话题,防止焦虑蔓延。