这是一个高一就应该掌握的内容,事实上很多高三学生都不清楚,拿这次二模考试的立体几何第一问证明来说,70%的学生竟然没有证得出来,即便证出来的也有很多是通过找特殊点做辅助线碰巧证出来的,脑海里并没有一个清晰的证明思路。
昨天问了一个学生他对此类问题的理解,他说没什么方法,就是看题目中的垂直条件,有的很容易看出来就会证,不太容易看出来的就听天由命了,之前写过一期高一立体几何的知识点和题型概括,文章内就有此类问题的解题思路和解题模型,链接为:,建议先看一下。
高三立体几何垂直的证明最难的是线与线的垂直证明,若证明线面垂直其实就告诉了方向,从所要证的平面内利用三垂线或三余弦定理可轻易找到所需的线;若证明面面垂直,只需从交线的角度分析也可找到所需的垂直条件,但在证明线线垂直时把哪条线放到平面内这是解题的关键,但很多学生并没有清晰的认识。
无论哪种垂直,最终都要转化到异面直线的垂直上,而异面直线垂直与否的判定是三垂线定理,即一定会用到投影的思想,而能否准确找到投影点才是解题的关键,此类问题就两种题型,两个方向,解释如下:
1.能准确找到投影点位置的。
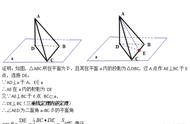
若证明l1⊥l2,若l1∈α,l2∈β,以l2为例,若l2在α上的投影能准确确定出,即l2在α上的投影点要么是确定的分点,要么是已知点,设投影为l3,则把l2,l3放到一个平面γ内,只需证明l1⊥平面γ即可,注意一定要找到线在面上的确切投影点,以课本上的习题为例:

直线AB1在平面AB B1A1中,本题根据条件能找到A1C在平面AB B1A1上的确切投影,投影为A1B,因此将A1B和A1C放到平面A1BC中,只需证明AB1⊥平面A1BC即可,当然由于题目的特殊性,找AB1在A1C所在平面的投影也可。

其中找投影的过程离不开题目中已知的垂直关系,以此为方向就知道如何处理直线所在的平面了。
2.找不到确切投影点位置的。
条件类似,若证明l1⊥l2,若l1∈α,l2∈β,若无法准确找到l1在平面β上的投影或无法找到l2在平面α上的投影,此时可从两条线所在的平面分析,以l1为例,若l1所在的平面α上能找到l3与l1垂直,则试着将l3和l2放到同一个平面γ内,只需证明l1⊥平面γ即可。
需要说明的是l1所在的平面可能不止一个,首先要猜测l1应该在的平面,再在平面上找另外一条与l1垂直的直线,这条直线由两点构成,两点要么是已知点,要么是特殊分点,很少会出现既非已知点又非特殊分点的情况。