由模型摘要表可知,R=0.989,说明自变量与因变量之间的相关性很强。
由ANOVA(方差分析)表可知F统计量的观测值为592.25,显著性概率为0.000,即拒绝原假设,说明因变量和自变量的线性关系是非常显著的,可建立线性模型。
由系数表可知回归模型的常数项为-4993.281,自变量“国内生产总值”的回归系数为0.197。因此,可以得出回归方程:财政收入=-4993.281 0.197 × 国内生产总值,回归系数的显著性水平为0.000,明显小于0.05,说明建立线性模型是恰当的。
02 非线性回归分析 SUNSHINE


步骤一:在菜单栏中找到分析→回归→非线性,打开“非线性回归”对话框;
步骤二:将“营业收入”移入因变量框,在模型表达式中输入相应的表达式;
步骤三:打开“参数”对话框,添加相应的参数值,点击确定。
Step 1
Analysis→Regression→Nonlinearinthemenubarandopenthe"NonlinearRegression"dialogbox;
Step 2
Move"businessincome"intothedependentvariablebox,andenterthecorrespondingexpressioninthemodelexpression;
Step 3
Openthe"Parameters"dialogbox,addthecorrespondingparametervalues,andclickOK.
输出窗口信息如下:
由迭代历史记录表可知,经过4次迭代后,模型达到收敛标准,找到了最佳解。得到营业收入关于两种广告费用的预测回归模型为:
y = 86.531 1.089x1-0.667x2 0.724x1x2
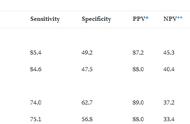
由显著性检验结果表可知,决定系数R2为0.941,拟合结果较好。
参考资料:百度百科,Google翻译
本文由LearningYard学苑原创,部分文字、图片来源于网络,如有侵权,请联系删除!
,