玻尔的原子结构模型
氢原子光谱与原子结构模型
氢原子是最简单的原子。若在真空放电管中充入少量氢气,通过高压放电,能发出不同波长的光,利用三棱镜可观察到不连续的线状光谱。
1885年,瑞士一位中学教师巴尔末(J. J. Balmer)在研究氢原子的可见光谱时发现,氢原子的可见光谱谱线的波长符合一定规律,他将其归纳为数学公式:

式中 B为一常数。这组谱线称为巴耳末线系。当n→∞时,λ→B,为这个线系的极限,这时邻近二谱线的波长之差趋于零。下图是巴耳末线系的示意图。(后来也有其他人的研究,可以搜索“氢原子光谱”)


汤姆生和卢瑟福的学生——玻尔分析了巴尔末的研究。他认为,巴尔末能用数学公式表示出氢原子光谱谱线长度,说明氢原子光谱的产生必有它的结构原因。受普朗克量子论和爱因斯坦光子学说的启发,玻尔吸收了卢瑟福的原子有核模型的合理成分,于1913年提出了新的原子结构假说,较好地解释了氢原子线状光谱的特征,因此获得1922年的诺贝尔物理学奖。
玻尔原子结构模型也存在着局限性,如该模型无法解释氢原子线状光谱的精细结构,也不能解释多电子原子的光谱。
电子运动不遵循宏观物体的运动规律,那么如何描述原子核外电子的运动状态?
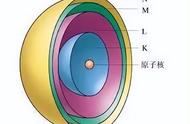
采用统计方法来描述电子在原子核外某一区域出现的机会。电子在原子核外空间出现的机会是有规律的。如氢原子的核外电子,当处于能量最低状态时(基态),电子主要在原子核周围的球形区域内运动,即距离核近电子出现机会大,距离核远电子出现机会小。