π
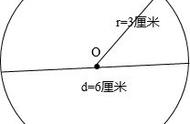
现在人们已经利用电子计算机将π的值算到了小数点后几万亿个,但最根本的原理,和第一个计算它的人并没有区别。后来人们发现圆的面积也和神奇的π有关系,得出了圆的面积公式S=πr²,然后进一步推导出圆柱体的体积公式V=πr²h,圆锥体的体积公式V=1/3πr²h,球体的体积公式V=4/3πr³···

球体的体积公式积分推导过程
有了这些公式,人们分土地、造柱子、做各种模具,就都有了科学依据。这一切,都是因为发现了π。
3.勾股定理a² b²=c²(a、b为直角三角形的两条直角边边长,c为斜边边长)。提出者:商高、毕达哥拉斯。

勾股定理
据公元前1000年左右的西周时代的《周髀算经》记载,商高:“故折矩,勾广三,股修四,经隅五。”这是勾股定理的最早描述,早于毕达哥拉斯定理五六百年,但是并未形成定理,着实可惜。

《周髀算经》
讨厌数学的人可能会说,不就是个特殊的直角三角形的规律吗?有什么了不起的?非也非也,勾股定理开启了用代数思想解决几何问题的大门,是数形结合的纽带。