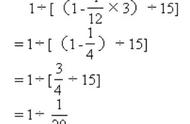分数四则混合运算
1.运算顺序:
(1) 同级运算,从左到右。
小技巧:可以随便调换位置,但要连同数字前面的运算符号一起调换。
对于二级运算,遇“÷”先变“ ×”,除数变倒数,“一线到底”约分到最简分数。所谓“一线到底”,在加减法中,先通分再计算; 在乘除法中,遇“除” 变“乘”,一次性约分,约到不能再约分为止。
(2) 异级运算,先乘除,后加减。
(3) 有括号,要先算小括号里面的,再算中括号里面的,最后算中括号外面的。
2.简便运算。
在分数四则混合运算中,可以运用整数运算律,使计算简便。
加法交换律:a b=b a
加法结合律:(a b) c=a (b c) 乘法交换律:ab=ba
乘法结合律:(ab)c=a(bc) 乘法分配律:a(b c)=ac bc 3.审题技巧。
分数乘法的意义在文字题中是个“陷阱”,如比 5 吨多是多少吨?
这道题中的“比 5 吨多”不是“差比”,而是“倍比”,一不小心就会列成 5 ,正确的列式为 5 5×。
4. 用方程解文字题是一种顺向思维的列式,在解决问题过程中可以把未知数用 x 代替,找出等量关系,然后把 x 作为已知量参与运算,最终得到等式求出未知量。
典例讲解
修一条路,第一天修了全长的 ,第二天修了全长的 ,第一天比第二天多修了 300 米,这条路长多少米? 思路分析:
根据“第一天比第二天多修了 300 米”可以列出等量关系式,即“第一天修的长度-第二天修的长度=300 米”,把全长看作单位“1”,列出方程计算。
除了学过的运算律,还可以用下面的方法简算。
减法的性质:
a-b-c=a-(b c)或 a-(b c) =a-b-c 除法的性质: a÷b÷c=a÷(b×c)或
a÷(b×c)= a÷b÷c正确区分分数和分率, 才能解答正确。
首先判断单位“1”的量:
知道单位“1”的量(用乘法),
不知道单位“1”的量(用除法),为确定解题方法奠定基础; 然后会把“比”字句转化成“是” 字句;最后能将省略式的分率句换说成比较详细的句 子的能力。
未知数的设法:
在分数应用题中,我们设单位“1”为 x; 在有比的问题中,设 1 份数为 x;在有和的问题中,设其中任意一个为 x,比如说两个班共有 50 人,设其中一个班有 x 人,则另一个班就有(50-x)人。
5. 分数应用题主要讨论的是以下三者之间的关系:
(1)分率:表示一个数是另一个数的几分之几,这几分之几通常称为分率。
(2) 标准量:解答分数应用题时,通常把题目中作为单位“1” 的那个数,称为标准量。(也叫单位“1”的数量)
(3) 比较量:解答分数应用题时,通常把题目中同标准量比较的那个数,称为比较量。(也叫分率对应的数量)
6. 分数应用题的分类。
(1) 求一个数的几分之几是多少。(解这类应用题用乘法) 这类问题特点是已知单位“1”的数量,求它的几分之几是多少,它反映的是整体与部分之间的关系。
(2) 已知一个数的几分之几是多少,求这个数。(解这类应用题用除法)这类问题特点是已知一个数的几分之几是多少,求单位“1”的量。
(3) 求一个数是另一个数的几分之几。(解这类应用题用除法)这类问题特点是已知两个数量,比较它们之间的倍数关
系。
7. 稍复杂的分数问题:
(1) 已知甲数,乙数比甲数的几分之几多(或少)多少,求乙
解决分数应用题时: 先要弄清两个概念:带单位的分数和不带单位的分数。带单位的分数,如 吨, 叫数量,表示一个物体的具体的数量。不带单位的分数,如 ,叫分率,它表示一个数的几分之几。
应用题解题思路:
第一步:确定单位“1”。找单位“1”的方法:找到题中不带单位的分数的那句话,“谁”的几分之几,那个“谁”就是单位“1”。
第二步:确定乘除法 。直接或间接告诉单位“1”的或可直接算出单位“1”的,用乘法;单位“1”是未知, 用除法。第三步:列式。 第四步:检查数。
(2) 已知总数,甲数是总数的几分之几,乙数是总数的几分之几,求甲数、乙数的和或者差。(两种关系式,两种思路)
(3)已知总数,其中甲数是总数的几分之几,求剩下的。(两种关系式,两种思路)
(4) 已知甲数和乙数比甲数多(或少)几分之几,求乙数。 (两种关系式,两种思路)
(5) 已知一个数的几分之几是多少,求这个数,既可以用除法计算,也可以列方程解答。
,