1.力的合成的规律
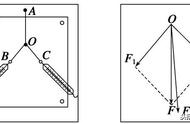
(1)平行四边形定则:两个力合成时,如果以表示这两个力的有向线段为邻边作平行四边形,这两个邻边之间的对角线就代表合力的大小和方向。
(2)三角形定则:把两个矢量首尾相接,从第一个矢量的始端指向第二个矢量的末端的有向线段就表示合矢量的大小和方向。三角形定则与平行四边形定则实质上是相同的。

2.两个力的合成
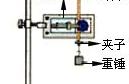
(1)作图法:根据平行四边形定则用作图工具作出平行四边形,然后用测量工具测量出合力的大小、方向,具体操作流程如下:

(2)计算法
①两分力共线时
a.若F1与F2方向相同,则合力大小F=F1+F2,方向与F1和F2的方向相同。
b.若F1与F2方向相反,则合力大小F=|F1-F2|,方向与F1和F2中较大的力的方向相同。
②两分力不共线时:可以先根据平行四边形定则作出分力及合力的示意图,然后由几何知识求解合力。
以下为求合力的三种常见特殊情况:


(3)合力大小与两分力夹角的关系
合力的大小不一定等于分力大小的代数和,也不一定比分力大。合力可以大于分力,也可以等于分力,还可以小于分力。两个大小一定的力进行合成时,合力的大小与两分力夹角θ的关系是:θ(0°≤θ≤180°)越大,合力越小;合力F的范围是:|F1-F2|≤F≤F1+F2。
3.多个力的合成
(1)合成方法:多个力的合成的基本方法仍然是平行四边形定则。具体做法是先求出任意两个力的合力,再求出这个合力跟第三个力的合力,直到把所有的力都合成进去,最后得到的结果就是这些力的合力。
(2)合成技巧:求解多个力的合力时,一般常见的合成技巧如下:
①将共线的力合成(方向相同或相反)。
②将相互垂直的力合成。
③将两个大小相等、夹角为θ(一般为60°或120°)的力合成。
④将两个夹角θ>90°且大小满足F1/F2=sin(θ-90°)的力合成(合力F与F1垂直)。
(3)三个力的合力范围的确定
①最大值:三个力方向均相同时,合力最大,Fmax=F1+F2+F3。
②最小值
a.若一个力在另外两个力的和与差之间,则它们的合力的最小值为零。
b.若一个力不在另外两个力的和与差之间,则它们的合力的最小值等于三个力中最大的力减去另外两个力。
值得注意的是:
F3的大小介于F1、F2的和与差之间,也可以说成是任意两个力的大小之和大于第三个力的大小,任意两个力的大小之差小于第三个力的大小,即三个力的大小具有的特点和三角形三边长度具有的特点相同,这时三个力的合力的最小值为零。
作图法与计算法的比较
(1)作图法简单、直观,但不够精确;计算法结果精确。
应用作图法时,各力必须选定同一标度,并且合力、分力比例适当,分清虚线和实线。
(2)计算法一般只用于特殊情况下求合力,作图法适用于所有情况。