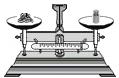
相反,如果你是一个躺在高速加速火箭里的一名宇航员,在你身上的接触力和你必须去做的努力来支撑你的身体(例如,保持正常的呼吸)显著增加,这将再次由一副你和你座位之间的秤显示出。接触阵营会说你看到漂浮在航天飞机里面或者拴在哈勃望远镜外面的宇航员都是失重的,在火箭发射过程中宇航员的重力剧增,但仍需努力保持头脑清晰。一个物体的重力通过一副置于物体和支撑面之间的秤会被不断地被修正。我们当然可以把秤放在任何地方,但是如果放在能取最大读数值的地方,这最大值就是物体的重力。

mg阵营对重力的定义
(不同于重力的日常意义)
一些物理学家将一个物体的重力定义为在此之上的重力,而不考虑其他的。他们的定义是“一个物体的重力是它的质量乘以当地的重力加速度。”这种重力的概念与物体的运动状态无关,并不考虑任何接触力。它并不等同于你刚刚坐在椅子上读这篇文章时的重量感,除非你分别坐于南极或者北极。

物理学家用这种定义重力的方式会把接触力作为“视重力”。虽然他们会说当你正在自由落体的重力和你坐在椅子上的一样,但是他们会补充到在自由落体时,你的视重是0。会说漂浮在航天飞机里面或者拴在哈勃空间望远镜外面的宇航员有着同在地球时一样的重力(低于地表400km地方略低于g),但是他们的视重为0。他们会说在火箭发射过程中努力保持头脑清晰的宇航员,有着相当于在家里厨房一样重力,但视重力会增加。
地球用一个“重力”的力(总是等于mg)拉着m的质量,表格中用标有“视重”的接触力支撑着m的质量。应用牛顿的“F = ma”给出下列:
重力(即mg)-视重=m×a(加速度)

依旧,在惯性坐标系中测量加速度。随着地球转动,如果物体不在两极上的话,加速度是不会等于0,其重力也不完全等同于视重。
mg阵营对重力的定义与非物理的重力定义一致,即当物体放置在重力场,但不在惯性坐标系里加速。例如,位于在地球的两极上的物体重力。