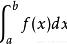定积分上限减下限是什么定理（定积分的定义中积分上下限看哪里） - 原点资讯

定积分上限减下限是什么定理,定积分的定义中积分上下限看哪里(1)

前面不定积分是求原函数，而今天的定积分是求和式极限，将两者关联起来的是牛顿-莱布尼兹公式。定积分常用于求平面图形的面积，变速直线运动路程和变力做的功。

第1节：定积分的概念和性质

定义：设函数f(x)在区间[a,b]上有定义，J∈R，若对任意ε>0 都存在σ>0，使得对[a,b]的任何分割T:a=x0<x1<x2<...<xn-1<xn=b，以及取任意介点值{ξi|xi-1≤ξi≤xi}，只要||T||<σ，就有|Σ(f(ξi)Δxi)-J|<ε，那么就称f(x)在[a,b]上可积，区间称为积分区间，a,b分别称为积分下，上限。也有称为黎曼可积，黎曼积分，黎曼和。
可积的必要条件定理：f(x）在[a,b]上可积，则函数在该区间必有界
定积分线性性质定理，与不定积分很像：设f(x) ,g(x)在I上都在[a,b]上可积，α，β为两任意实常数，则αf(x) βg(x)在区间上也可积且∫[αf(x) βg(x)]dx =α∫f(x)dx β∫g(x)dx |积分上限b,积分下限a
可积的充要条件定理：f(x）在[a,b]上可积 <==>对任意c∈(a,b)，f(x)在[a,c]与[c,b]上都可积，此时有等式∫f(x) dx |a->b = ∫f(x) dx |a->c ∫f(x) dx |c->b。这个也叫积分区间的有限可加性
定理：满足可积条件下，|∫f(x) dx |a->b | = ∫|f(x)| dx |a->b ，即积分的绝对值 = 函数值的绝对值的积分

定积分上限减下限是什么定理,定积分的定义中积分上下限看哪里(2)

第2节：微积分基本定理 ,在这节内容，会感受到函数连续性的重要性

变上限定积分与变下限定积分，简单来说就是积分上限或者下限是变量。型如，F(x)=∫f(t) dt |a->x ，x∈[a,b]
定理：若f(x)在[a,b]上可积，则其变上限积分所定义的函数F(x) 在[a,b]上连续。关联了可积与连续性
原函数存在定理：设f(x)在[a,b]上连续，则变上限定积分所定义的函数F(x)是f(x)在[a,b]上的原函数，即F`(x)=d*∫f(t) dt |a->x /dx = f(x) x∈[a,b]。关联了原函数与连续性
推论：设f(x)在[a,b]上连续，则d*∫f(t) dt |x->b /dx = -f(x)。
连续函数的可导且复合函数是有意义的。即积分上限是一个关于x的函数
微积分基本定理-牛顿莱布尼兹公式：设f(x)在[a,b]上连续，F(x)是f(x)在[a,b]上的一原函数，即F`(x)=f(x)，则∫f(x) dx |a->b = F(b)-F(a)

定积分上限减下限是什么定理,定积分的定义中积分上下限看哪里(3)

第3节：定积分的计算，主要讲常见的定积分计算的类型，没有太多理论性的东西。可以对比不定积分的计算

第4节：讨论定积分存在的条件

布达和的概念，包括布达上和S，布达下和s。其实就是同一分割下，最大与最小的积分和
上下和性质定理1：满足条件的同一分割下，上和是所有积分和的上确界，下和是所有积分和的下确界
上下和性质定理2：在分割T下增加分割点所得新分割T`,相比以前，下和递增，上和递减
上下和性质定理3：任意两分割组合成一个新分割，新上和不超过之前的任意一个分割的上和，新下和≥之前的任意一个分割的下和
上下和性质定理4：对任意两分割，总有下和不超过上和
布达定理：lim s(T)=s ||T||->0 ；lim S(T)=S ||T||->0
可积准则1：设f(x)在[a,b]上有界，则f(x)在[a,b] 可积<==> f(x)在[a,b]的上积分=下积分，即S=s
可积准则2：设f(x)在[a,b]上有界，则f(x)在[a,b] 可积<==>对任意ε>0,总存在一分割T，使得 S(T)-s(T)<ε
可积准则3：设f(x)在[a,b]上有界，则f(x)在[a,b] 可积<==>对任意正数ε，η，总存在一分割T，使得属于T的所有小区间中，对应于振幅wk`≥ε的那些小区间的总长ΣΔxk`<η
可积函数类1：在闭区间连续的函数可积
可积函数类2：在闭区间单调的函数可积
可积函数类3：在闭区间只有有限个间断点的有界函数可积

第5节：积分中值定理