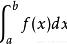今天是高等数学第11篇文章,我们来看看定积分的相关内容。
对于很多人来说定积分的内容其实早在高中就已经接触过了,比如在高中物理当中,我们经常使用一种叫做”微元法“的方法来解决一些物理问题。但实际上所谓的”微元法“本质上来说其实就是一种微积分计算方法。我们来看两个简单的例子。
微分与积分的例子
第一个例子是扇形的面积计算,先别急着笑,我知道这个是初中的内容。扇形的面积谁不会算,扇形的面积等于圆的面积乘上圆心角嘛。

圆的面积我们都知道 πr^2,如果是扇形的话,再加上圆心角,我们用弧度制来表示圆心角,可以直接进行计算:πrθ。
除此之外还有别的办法吗?
当然是有的,我们来看下面这张图:

在下面这张图当中,我们从扇形上切了一小块出来,做了一个直角三角形。我们令这个直角三角形无限窄,那么它的面积就可以近似于这一块小扇形的面积。
直角三角形的面积很简单,我们都会算,我们令短的直角边长度是l。那么这个小三角形的面积就等于1/2 rl。
我们如此操作,可以把这一块扇形分割成无数个这样的小三角形,最后我们把这些小三角形的面积全部加起来,就可以得到扇形的面积。由于l趋向于0,每一个小三角形和小扇形的面积差的极限都是0,所以可以近似看成它们相等。
这样一番操作之后,我们可以用无数个小三角形的面积来代替扇形的面积。对于这些小三角形而言,它们的面积都是1/2 rl。把它们进行累加,本质上也就是把这些所有的短边进行累加。那么显然,这些所有的短边累加之后的结果就是扇形的弧长。
我们假设这块扇形的弧长是L,那么整个扇形的面积还可以表示成1/2rL。
我们可以简单验证一下,一个完整的圆也可以看成是一个扇形。一个完整的圆,它的弧长,也就是周长是2πr。我们代入刚才的公式,得到的结果和圆的面积公式吻合,所以我们的计算是正确的。
在这个例子当中扇形分割成的每个小三角形是一样的,所以我们可以直接进行累加。如果我们微分之后的结果不再是固定的,是变化的,那么应该怎么办?
我们再来看另外一个例子:

比如我们要求a和b两点围成的曲线矩形的面积,我们也可以将矩形进行拆分。我们可以无限拆分成多个小的矩形的面积去替代。我们可以很容易证明,当Δx趋向于0的时候,那一块小的矩形面积和曲线矩形的面积相等。所以我们可以把它拆分成无数个这样的矩形,然后将所有的面积求和,就得到了曲线围成的面积。
对于每一块矩形而言,它们的宽都是Δx,但是它们的高都不相同。但是很容易看出来,它们的高都是区间里某一个坐标的函数值。其实我们可以写出来这些序列的值,它们分别是: a, a Δx, a 2Δx, ..., b。
为了方便书写,我们令这个序列等于 {ζ1, ζ2, ζ3 ... ζn} 所以曲线围成的面积可以写成: