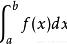定积分的定义
我们观察一下上面这个问题,其实我们知道了很多信息,比如我们知道了函数f(x),我们还知道了a和b的值,看起来已经离结果很近了。的确如此,但是在我们继续往下之前,我们必须要明确一点,我们这样的推算是有前提的。
最大的也是隐藏的前提就是我们做的划分,我们必须要保证两点,首先我们要保证当Δx趋向于0的时候,矩形高度的极限是确定的。并且这些小矩形的面积和的极限趋近于它真实的面积。
我们用数学的语言来表达,也就是说,我们无论如何选取每一个ζi,我们都要保证

是一个定值,这样我们就可以把这个式子写成定积分的形式:

这里的f(x)称作被积函数,f(x)dx称为被积表达式,x叫做积分变量,a和b分别称为积分的上限和下限。
如果f(x)在[a, b]上的定积分存在,那么就称为f(x)在区间[a, b]上可积。
什么样的函数可积呢?
这个问题要用数学的语言证明不太容易,但是如果从直观上去理解则要简单很多。通过上面的图,我们很轻松可以得到结论:连续函数一定可积,并且如果函数在[a, b]上有界并且只有有限个断点也可积。因为有限个间断点不会影响面积的计算,从这个角度入手,是否可积的判断其实还是很好理解的。
我们明白了可导的定义之后,我们再把之前连续和可导这些性质串起来,我们就可以编出高数顺口溜了:
可导一定连续,连续不一定可导。
连续一定可积,可积不一定连续。
可导一般可积,可积不一定可导。
理解并且记住这个顺口溜可是学好高数的基础,不信可以去问问考研党,这几句必然朗朗上口。如果觉得晕头转向也没关系,以后有机会会单独开一篇文章好好讲讲这几个顺口溜。
简单性质
最后,我们来看下定积分的一些简单性质。
第一个是加法性质:

这个很好证明,我们只需要将它转化成累加的形式就可以把括号里相加的内容拆开: