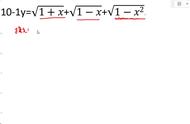根号5又可怎样表示,根号5数值

即√7可以用下图中的连分数来表示：

简记为√7=[2,1,1,1,4,1,1,1,4...]=[2,1,1,1,4]，其中1,1,1,4表示以1,1,1,4为循环节。

以√n为例

• 将√n分离为整部z1和分部f1
• 求分部f1的倒数d1
• 将d1分离为整部z2和分部f2
• 求分部f2的倒数d2
• 将d2分离为整部z3和分部f3
• 重复上述过程，直到分部fn第一次和前面某分部fk相同（fn=fk）为止，结束过程分离。
• √n=[z1，z2，。。。zi，。。。，zn]

按上述操作，将√13化为连分数

1. 分离√13=3 (√13-3)，得z1=3,f1=√13-3；
2. d1=1/(√13-3)=(√13 3)/4;
3. 分离d1,得z2=1,f2=(√13-1)/4；
4. d2=4/(√13-1)=(√13 1)/3;
5. 分离d2,得z3=1,f3=(√13-2)/3；
6. d3=3/(√13-2)=(√13 2)/3;
7. 分离d3，得z4=1，f4=(√13-1)/3；
8. d4=3/(√13-1)=(√13 1)/4;
9. 分离d4，得z5=1，f5=(√13-3)/4；
10. d5=4/(√13-3)=√13 3=6 (√13-3);
11. 分离d5，得z6=6，f6=√13-3
12. 分部第一次出现重复f1=f6，分离过程结束。
13. √13=[3,1,1,1,1,6]

用《几何画板》验证：

即

按上述操作，将√101化为连分数

1. 分离√101=10 (√101-10)，得实部10,分部(√101-10)；
2. 分部的倒数1/(√101-10)=√101 10;
3. 分离√101 10,得实部20,分部√101-10；
4. 分部第一次出现重复，分离过程结束。
5. √101=[10,20]

即