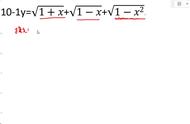渐进分数表示了向无理数逐渐逼近无理数的趋势,所以渐近分数可以用来表示无理数的近似值。
如√3=[1,1,2]的前五个渐近分数:
A1=[1]=1,
A2=[1,1]=2,
A3=[1,1,2]=1 2/3≈1.667,
A4=[1,1,2,1]=1 3/4≈1.75,
A5=[1,1,2,1,2]=1 8/11≈1.73。
再如√101=[10,20]的前三个渐近分数:
A1=[10]=10,
A2=[10,20]=10 1/20=10.05,
A3=[10,20,20]=10 20/401≈10.04988。
1761年,德国数学家兰伯特证明了圆周率pi是无理数,因而pi也可以用连分数来表示(计算过程太复杂,略)
pi=[3,7,15,1,292,1,1...]
pi的前四个渐近分数:
A1=3,
A2=22/7,
A3=333/106,
A4=355/113。
其中,A2,A3恰好分别是祖冲之计算出的“约率”和“密律”。
05--结语拉马努金恒等式,揭示了用无理数表示有理数,用连分数表示无理数,说明无理数也可以用有理数来表示。因而有理数和无理数的种关系是辩证的统一,是符合辩证法的。
用连分数表示无理数的主要步骤:分离,求倒数。
无理数的渐近分数可以用来表示无理数的近似值,这也算用连分数表示无理数的用途之一吧。