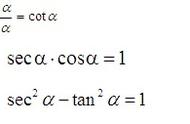梳理了前面三角基本概念,单位制,扇形与弧长公式,相信大家对三角的学习有了一个好的开始,要想真正的理解三角函数的内涵,还需要从一些口诀来入手,今天我们就来谈谈三角函数和诱导公式;
第一、三角函数的定义
三角函数的定义分初中(锐角三角比)高中(任意角三角函数),不同的学习阶段,对应不同的领悟层次需要。高中阶段主要研究的是正余弦正切函数,因此这三者定义以及函数图像及性质需要完全透彻的理解。

这些三角函数值在各个象限的符号如下图所示,

记忆的过程中可以结合三角函数函数线的定义以及动态来观察角α变化的过程中三角函数线的增长趋势。
第二、三角函数线
角α的三角函数值可以用单位圆的有向线段表示:sinα=MP,cosα=OM,tanα=AT.
有向线段MP,OM,AT分别叫做角α的正弦线,余弦线,正切线。

对于三角函数线的认知,我们需要关注以下几点:
(1)结合象限角以及有向线段在各个区间内分别讨论,而且需要注意三角函数线中的字母顺序不可颠倒,与坐标轴方向一致的有向线段为正,此时相应的三角函数值为正,与坐标轴方向相反的有向线段为负,对应的三角函数值为负。
(2)当角α的终边在x轴上时,正切线、正弦线变为一个点,角α的终边在y轴上时,余弦线变为一个点,正切线不存在。
(3)若果0<α<π/2,则sinα<α<tanα,sinα cosα>1。
第三、同角三角基本关系式
针对同一个角,结合三角比的定义,我们会发现,他有如下三种关系: