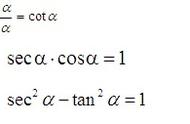针对上述正六边形,结合6个三角比,我们借助:“上弦,中切,下割,左正,右余,中间1”,这十三字,我们可以很快做好定位,不清楚的同学,可以评论区里留言。
具体如何应用这正六边形辅助记忆呢?
首先我们来看平方关系,上图3个红色阴影部分,大家可以视为3个倒三角,上底边的2个三角比的平方之和等于下底角的平方。
其次我们来看商数关系,看相邻三点,如下图,再结合上图,无论ABC,还是ABF,底边上的2个端点之任意一个端点,都等于中间顶点去除另外一个底点,如:tanα=sinα/cosα,cosα=sinα/tanα,secα=tanα/sinα,cscα=secα/tanα等等;

最后我们再看倒数关系,我们来找正六边形的对角线,对角线的两个端点的乘积就是中间1,构成了我们的倒数关系。

以上3个点,我们也可以用一段话来诠释:
对角线上两函数之积为1,任一角的函数等于与其相邻的两个函数的积,阴影三角形,顶角的两个函数的平方和等于底角函数的平方。
熟悉了同角三角关系式,在应用的过程中,我们还需要注意以下几点:三角函数值间的知一求二,或者求式子的值;化简三角函数式,证明三角恒等式等等。
第四、诱导公式:奇变偶不变,符号看象限

看了上图的表格,相信大家依然懵懂,不要紧,我们看看这个奇和偶,他是针对π/2,而言的,符号看的是左边原始式子,对于α,无论大小,均视为锐角,了解了这些,相信大家对于以下式子理解起来倍感轻松。