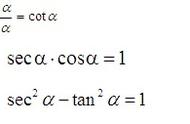一、同角三角函数的基本关系式:

二、三角函数的公式:
1、基本关系(共五组三角函数公式)

2、角与角之间的互换(函数公式共六组)

诱导公式重点记忆:“奇变偶不变,符号看象限”
三、三角函数图像的平移
对函数y=Asin(ωx+)+k (A>0, ω>0, ≠0, k≠0),
(1)振幅变换(纵向伸缩变换):是由A的变化引起的.A>1,伸长;A<1,缩短.
(2)周期变换(横向伸缩变换):是由ω的变化引起的.ω>1,缩短;ω<1,伸长.
(3)相位变换(横向平移变换):是由φ的变化引起的.>0,左移;<0,右移.
(4)上下平移(纵向平移变换): 是由k的变化引起的.k>0, 上移;k<0,下移
四、三倍角公式:

| 六边形记忆法:图形结构“上弦中切下割,左正右余中间1”;记忆方法“对角线上两个函数的积为1;阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方;任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。” |