题目(贵港中考题):
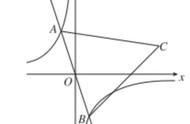
如图,过C(2,1)作AC//x轴,BC//y轴,点A,B都在直线y=-x 6上,若双曲线y=k/x(x>0)与△ABC总有公共点,则k的取值范围是________.

解析:
方法—:
当双曲线y=k/x(x>0)与△ABC的公共点为C(2,1)时,k=xy=2×1=2;
当双曲线y=k/x(x>0)与△ABC的唯一公共点在直线y=-x 6上时,
该公共点的横坐标即为关于x的方程k/x=-x 6的解,
因为公共点是唯一的,所以该方程,即x²-6x k=0有两个相等的实数根,
于是,得Δ=(-6)²-4×1×k=0,解得k=9;
由反比例函数中,比例系数k值的几何意义知,2是k的最小值,9是k的最大值;
综上,k的取值范围为:2≤x≤9.
故空中需填:2≤x≤9
方法二:
因为点C(2,1),BC//y轴,AC//x轴,
所以,当x=2时,y=-2 6=4,
当y=1时,-x 6=1,解得x=5,
所以,点A为(5,1),点B为(2,4),
由反比例函数中比例k的几何意义知,
当反比例函数的图象,过△ABC的顶点C(2,1)时,
k=2×1=2,
并且2是k的最小值;
设反比例函数的图象与直线AB相交于点(x,-x 6),
则k=x(-x 6)=-x² 6x=-(x-3)² 9,
因为2≤x≤5,
所以,当x=3时,k值最大,
此时交点坐标为(3,3),
此时k=9;
所以,k的取值范围为:2≤x≤9.
故空中需填:2≤x≤9
点拨:
1.熟悉k的几何意义;
2.熟悉一元二次方程的解与其根的判别式的关系;
3.熟悉把二次函数解析式配成顶点式的方法.
,