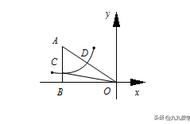
如图,一次函数y=﹣x 4的图象与反比例y=k/x(k为常数,且k≠0)的图象交于A(1,a),B两点.
(1)求反比例函数的表达式及点B的坐标;
(2)在x轴上找一点P,使PA PB的值最小,求PA PB的最小值.


考点分析:
反比例函数与一次函数的交点问题;轴对称﹣最短路线问题.
一次函数图象直线y=kx b位置与k,b的关系:
(1)k>0直线向上的方向与x轴的正方向所形成的夹角为锐角;
(2)k<0直线向上的方向与x轴的正方向所形成的夹角为钝角;
(3)b>0直线与y轴交点在x轴的上方;
(4)b=0直线过原点;
(5)b<0直线与y轴交点在x轴的下方;
题干分析:
(1)把点A(1,a)代入一次函数y=﹣x 4,即可得出a,再把点A坐标代入反比例函数y=k/x,即可得出k,两个函数解析式联立求得点B坐标;
(2)作点B作关于x轴的对称点D,连接AD,交x轴于点P,此时PA PB=PA PD=AD的值最小,然后根据勾股定理即可求得.