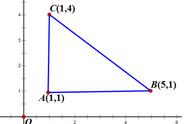
2. (2021九上·鄂城期末) 如图,已知A(1,m),B(2,n) 是反比例函数
图象上的两点,动点P(x,0)在x轴正半轴上运动,当 | AP - BP | 达到最大时,点P的坐标是_______

分析:通过反比例函数解析式可以先求出A、B两点的具体坐标,再连接AB,在△ABP中,利用三边关系-两边之差小于第三边来构造一个不等式,即| AP - BP |≤ AB,所以| AP - BP |的最大值就是AB,当且仅当A、B、P三点共线时,可取等号,也就是AB与x轴的交点,通过待定系数法可求出AB所在直线解析式,进而可以求得交点P坐标
解:
连接AB并延长,如图
A、B两点在反比例函数上,所以m=2,n=1,即A(1,2),B(2,1)
在△ABP中,| AP - BP |≤ AB,当A、B、P三点共线时,取等号,即此时点P是直线AB与x轴的交点
设AB所在直线解析式为:y=kx b
将A、B点坐标代入得

解得k=-1,b=3
所以直线AB的解析式为y=-x 3
令y=0,得x=3
所以此时P点坐标为(3,0)

视频讲解:
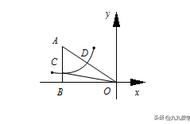
3. (2021九上·香洲期末) 等腰Rt△ABC和等腰Rt△ADE的腰长分别为4和2,
其中∠BAC=∠DAE=90°,点M为边DE的中点,若等腰Rt△ADE绕点A旋转,则点B到点M的距离最小值________