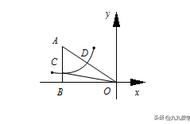
分析:连接AM,AM是Rt△ADE的中线,AB、AM的长度是固定的,在△ABM中利用三边关系可得AB - AM ≤ BM ≤ AB AM,即可求出BM的最大值和最小值。
另一种思路是分析点M的运动轨迹,A点是定点,AM是定长,会发现点M的运动轨迹是以点A为圆心,AM长为半径的圆,BM的距离就可以转化为圆上一点与圆外一点的距离问题
解:
方法一:

如图,连接AM,在Rt△ADE中,AM是中线,AE=DE=2,所以AM=
,在△ABM中由三边关系可得AB - AM ≤ BM ≤ AB AM,当B、A、M三点共线时可取等号,即

∴BM的最小值为4-
方法二:

由题意可知,点M的运动轨迹是以点A为圆心,AM长为半径的圆,连接AM,以A点为圆心,AM长为半径画圆,交AB于点M1,交BA的延长线于点M2,
在Rt△ADE中,AM是中线,AE=DE=2,
∴AM1=AM2=AM=
由图可得BM1 ≤ BM ≤ BM2
即AB - AM1 ≤ BM ≤ AB AM2
即