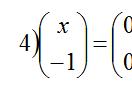这种办法可以算出各种阶数的行列式的值,大家照猫画虎地找几个行列式练练手,自然就学会了。
现在我给出余子式和代数余子式的数学定义:
把n阶行列式的第i行和第j列划去所得到的n-1阶行列式称为(i,j)位元素aij的余子式,记作Mij,称 Aij=(-1)^(i j)Mij 为 aij的代数余子式。
对某一行或列展开的行列式的值等于该行或该列的各元素与其代数余子式的乘积之和。
如果我上来就给大家讲这个概念的话,大家肯定会不知所以然。现在大家只要挨字挨句地读一遍,一下就明白了。(滑稽地说,我还真不知道大家愿不愿意看这个定义,反正我是懒得看它)
最后,我举个四阶行列式的例子完成今天的内容:

我随便编了一个四阶方阵
这里啰嗦一句,上面这个四阶行列式的意义是描述数学意义上四维斜空间的面积比率,注意,这个四维空间只有数学意义,是线性的,是在欧几里得公理体系里定义的;不要和非欧几何性质的四维时空混为一谈!

假想的四维空间(理论,纯数学)

真实的四维时空(非线性,物理)
用我们刚才学的东西,大家就能轻易知道: