我们的教科书上有这句性质,角平分线上的点到角两边的距离相等。但是在实际题目中,远远不够的,以下总结了考试中常出现的模型。
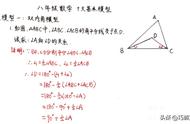
模型1:角平分线上的点向两边作垂线
这个模型的基本思想是过角平分线上一点 P 作角两边的垂线。如图中 PA⊥OA,PB⊥OB。容易通过全等得到 PA=PB(角平分线性质)。
注意:题目一般只有一条垂线,需要自行补出另一条垂线。甚至只给你一条角平分线,自行添加两条垂线。

模型1:角平分线上的点向两边作垂线
模型分析
利用角平分线的性质:角平分线上的点到角两边的距离相等,构造模型,为边相等、角相等、三角形全等创造更多的条件,进而可以快速找到解题的突破口。

模型2:截取构造对称全等
这个模型的基础是在角的两边分别截取 OA=OB,然后在对角线上取任意一点 P,连接 AP,BP。容易证得△APO≌△BPO。注意:一般这样的模型最容易被孩子忽略,因为这个模型里没有的角度,因而对于孩子而言添出 PB 这条辅助线是有难度的。
添加这条辅助线的基本思想是在 ON 上截取 OB,使得 AP=BP。从而构造出一个轴对称。这样的模型一般会出现在截长补短里。

模型2:截取构造对称全等
模型分析
利用角平分线图形的对称性,在角的两边构造对称全等三角形,可以得到对应边、对应角相等。利用对称性把一些线段或角进行转移,这是经常使用的一种解题技巧。