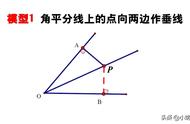
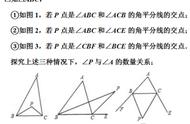
1、双中点线段等于两线段和或差的一半
2、双角平分线夹角等于两角和或差的一半
二、证明1、双中点模型
已知:A、B、C三点共线,D、E分别为AB、BC中点,求DE长.
(1)两线段无公共部分

∵D、E分别为AB、BC中点
∴DB=1/2AB,BE=1/2BC
∴DE=DB BE=1/2(AB BC)=1/2AC
无公共部分时,双中点线段等于两线段和的一半。
(2)两线段有公共部分

∵D、E分别为AB、BC中点
∴DB=1/2AB,BE=1/2BC
∴DE=DB-BE=1/2(AB-BC)=1/2AC
有公共部分时,双中点线段等于两线段差的一半。
2、双角平分线模型
已知:OD、OE分别平分∠AOB、∠BOC,求∠DOE.
(1)两个角无公共部分

∵OD、OE分别平分∠AOB、∠BOC
∴∠BOD=1/2∠AOB,∠BOE=1/2∠BOC
∴∠DOE=∠BOD ∠BOE=1/2(∠AOB ∠BOC)=1/2∠AOC
无公共部分时,双角平分线夹角等于两角和的一半。
(2)两个角有公共部分

∵OD、OE分别平分∠AOB、∠BOC
∴∠BOD=1/2∠AOB,∠BOE=1/2∠BOC
∴∠DOE=∠BOE-∠BOD=1/2(∠BOC-∠AOB)=1/2∠AOC
有公共部分时,双角平分线夹角等于两角差的一半。
三、应用对于刚接触几何的七年级学生来说,关于线段或角的计算是有很大难度的,这就要求学生面对这类题时具有一定的思路,知道大概的思考方向。一般来讲,这类题通常由问题出发,先由线段和差或角的和差确定解题方向,然后辅以线段中点或角平分线来解决。
但是,对于有公共部分的双中点线段或双角平分线模型,可以写出的线段和差或角的和差种类较多,这就增加了思考的难度。如果掌握了这两个模型的结论,那就可以快速选取正确的线段和差或角的和差,迅速解题,如果是填空选择,则可以直接口算出答案。
总之,基本模型的掌握既可以快速得出小题的答案,又可以为大题的解决确立方向。

同学们可以试着做下上一篇中的前两问,顺便复习一下第三问。
四、小结1、无图或动点问题,往往要分类讨论;
2、要注重基本模型及解题思路的积累。
,