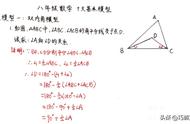
模型3:角平分线 垂线构造等腰三角形
这个模型的基础是,在角平分线上任意找一点 P,过点 P 作角平分线的垂线交角的两条边与A、B。这样就构造出了一个等腰三角形AOB,即 OA=OB。这个模型还可以得到P是AB中点。
注意:这个模型与一之间的区别在于垂直的位置。并且辅助线的添加方法一般是延长一段与角平分线垂直的线段。如图中的 PB。

模型3:角平分线 垂线构造等腰三角形
模型分析
构造此模型可以利用等腰三角形的“三线合一”,也可以得到两个全等的直角三角形,进而得到对应边、对应角相等。这个模型巧妙地把角平分线和三线合一联系了起来。

模型4:角平分线 平行线
这个模型是在角平分线上任意找一个点 P。分别过点 P 作 ON,OM 的平行线 PA, PB。通过角平分线和平行线就可以构成两组等腰三角形 OAP 和 OBP,还能知道四边形OBPA 是一个平行四边形。

模型4:角平分线 平行线
模型分析
有角平分线时,常过角平分线上一点作角的一边的平行线,构造等腰三角形,为证明结论提供更多的条件,体现了角平分线与等腰三角形之间的密切关系。