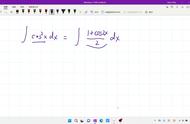
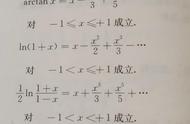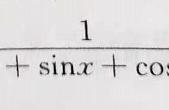求不定积分时,用的方法不同,就有可能得到不同的形式的原函数。不过这些不同形式的原函数,是可以通过转化成为同一种形式的。这种情况特别多见于与三角函数有关的不定积分中。

比如正割函数的不定积分,就至少可以用三种方法,求出三种形式。为了让大家感受后两种解法的强大功能,老黄决定先从最繁的方法解起。
问题:求∫secxdx.
解法1:原积分=∫dx/cosx【依据:secx=1/cosx】
=∫dx/((cos(x/2))^2-(sin(x/2))^2)【依据:cos2x=(cosx)^2-(sinx)^2,记为公式(1),下面还有用】
=1/2*∫((cos(x/2) sin(x/2))/(cos(x/2)-sin(x/2)) (cos(x/2)-sin(x/2))/(cos(x/2) sin(x/2)))dx【反过来从后往前转化,将括号内通分相加,就可以检验它的正确性,这一步全靠经验的支持,注意不定积分前多了系数1/2。】
=1/2*(∫(cos(x/2) sin(x/2))/(cos(x/2)-sin(x/2))dx ∫(cos(x/2)-sin(x/2))/(cos(x/2) sin(x/2))dx)【运用了和的积分等于积分和的线性法则】
=-∫(d(cos(x/2)-sin(x/2))/(cos(x/2)-sin(x/2)) ∫(d(sin(x/2) cos(x/2)))/(cos(x/2) sin(x/2))【这一步凑微分,很有技术感。两个不定积分同时凑微分。注意,不定积分前面的系数1/2在凑微分时,被用掉了】
=ln|(cos(x/2) sin(x/2))/(cos(x/2)-sin(x/2))| C.【这里运用了∫du/u=ln|u|,换元总是在悄无声息中完成的。另外还运用了lna-lnb=ln(a/b)】
=ln|(1 sinx)/cosx| C.【分子分母同时乘以分子,分母运用了平方差公式以及公式(1),分子运用了完全平方公式,以及sin^2 cos^2=1,和2sinxcosx=sin2x】

这是第一个结果:∫secxdx=ln|(1 sinx)/cosx| C.
再看第二次解法,没有对比就没有伤害,你可以看到它有多简便。
解2:原积分=∫cosx/((cosx)^2)dx【欲擒故纵,先化得复杂点,然后再搞定它】
=∫dsinx/(1-(sinx)^2)【悄无声息的完成了凑微分】
=1/2*ln|(1 sinx)/(1-sinx)| C.【这里运用了积分公式∫dx/(1-u^2)=1/2*ln|(1 u)/(1-u)| C.换元又在悄无声息中完成的。】

这就得到了第二个结果:∫secxdx=1/2*ln|(1 sinx)/(1-sinx)| C.
如果你嫌解法2还要运用到其它积分公式的话,放心,还有解法3. 他既简便,也无需运用到其它积分公式,简直可以简便到毁你的三观。就是需要一点脑筋才能想得到。
解3:原积分=∫(secx(secx tanx))/(secx tanx)dx【还是欲擒故纵,声东击西,这回化得更复杂,但是把分子的括号展开,分配律用起来,就会发现,分子正好是分母的微分】
=∫(d(tanx secx))/(secx tanx)dx=ln|secx tanx| C.【简单到毁三观吧!】

这就得到了原积分的三种不同的形式:
∫secxdx∫secxdx=ln|(1 sinx)/cosx| C=1/2*ln|(1 sinx)/(1-sinx)| C=ln|secx tanx| C.
其中第(1)(3)种形式很明显可以看出是一致的。关键是形式(2)要怎么转化成形式(1)或形式(3).
其实也很简单的,只要转换√|(1 sinx)/(1-sinx)|成|(1 sinx)/cosx|就可以了。形式(2)分子分母同时乘以√(1 sinx),分母为√(1-(sinx)^2)=|cosx|成立;分子为√(1 sinx)^2=|1 sinx|,同样是成立的。因此虽然三个结果形式不同,但它们是可以统一成一个形式的。以后看到别人求的不定积分结果和你的形式不同,就不要轻易说别人求错了哦。