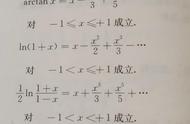三角函数有理式R(sinx,cosx)是由sinx,cosx及常数作为运算单元,经有限次的加减乘除得到的函数,它的积分使用万能代换t=tan(x/2)都可以化为有理函数的积分。万能代换对于此类积分尽管具有普遍性,但是解题过程过于繁琐。对于某些特殊情况可不使用万能代换,也可将此类积分化为有理函数的积分,通常的方法如下:
(1)若R(sinx,-cosx)=-R(sinx,cosx)(关于cox是奇函数),则可令t=sinx;
(2)若R(-sinx,cosx)=-R(sinx,cosx)(关于sinx是奇函数),则可令t=cosx;
(3)若R(-sinx,-cosx)=R(sinx,cosx),则可令t=tanx;
题型一:利用万能公式求解
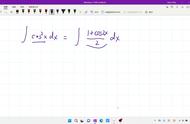
例1:

分析:解决三角函数有理式的基本方法就是万能公式。
解:

题型二:若R(sinx,-cosx)=-R(sinx,cosx)(关于cox是奇函数),则可令t=sinx;
例2:

解:

题型三:若R(-sinx,-cosx)=R(sinx,cosx),则可令t=tanx;
例3:

解: