静力学
静力学是研究物体在力系作用下平衡的科学。
第一章、静力学公理和物体的受力分析
教学目标:掌握物体的受力分析和正确画出受力图。
知识结构:
1、 基本概念:力、刚体、约束和约束力的概念。
2、 静力学公理:
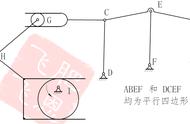
(1)力的平行四边形法则;(三角形法则、多边形法则)注意:与力偶的区别
(2)二力平衡公理;(二力构件)
(3)加减平衡力系公理;(推论:力的可传性、三力平衡汇交定理)
(4)作用与反作用定律;
(5)刚化原理。
3、常见约束类型与其约束力:
(1)光滑接触约束——约束力沿接触处的公法线;
(2)柔性约束——对被约束物体与柔性体本身约束力为拉力;
(3)铰链约束——约束力一般画为正交两个力,也可画为一个力;
(4)活动铰支座——约束力为一个力也画为一个力;
(5)球铰链——约束力一般画为正交三个力,也可画为一个力;
(6)止推轴承——约束力一般画为正交三个力;
(7)固定端约束——两个正交约束力,一个约束力偶。
4、物体受力分析和受力图:
(1)画出所要研究的物体的草图;
(2)对所要研究的物体进行受力分析;
(3)严格按约束的性质画出物体的受力。
注
意点:(1)画全主动力和约束力;
(2)画简图时,不要把各个构件混在一起画受力图;
(3)灵活利用二力平衡公理(二力构件)和三力平衡汇交定理;
(4)作用力与反作用力。
第二章、平面汇交力系与平面力偶系
教学目标:掌握平面汇交力系和平面力偶系的合成与平衡的计算方法。
知识结构:
1、平面汇交力系:
(1)几何法(合成:力多边形法则;平衡:力多边形自行封闭)
(2)解析法(合成:合力大小与方向用解析式;平衡:平衡方程
,
)
注
意点:(1)投影轴尽量与未知力垂直;(投影轴不一定相互垂直)
(2)对于二力构件,一般先设为拉力,若求出负值,说明受压。
2、平面力对点之矩——
,逆时针正,反之负
注
意点:灵活利用合力矩定理
3、平面力偶系:
(1)力偶:由两个等值、反向、平行不共线的力组成的力系。
(2)力偶矩:
,逆时针正,反之负。
(3)力偶的性质:
[1]、力偶中两力在任何轴上的投影为零;
[2]、力偶对任何点取矩均等于力偶矩,不随矩心的改变而改变;(与力矩不同)
[3]、若两力偶其力偶矩相等,两力偶等效;
[4]、力偶没有合力,力偶只能由力偶等效。
(4)力偶系的合成(
)与平衡(
)
第三章、平面任意力系
教学目标:掌握平面任意力系的简化与平衡力系的计算方法,会计算平面桁架的内力。
知识结构:
1、力的平移定理:把力向某点平移,须附加一力偶,其力偶矩等于原力对该点的力矩。
2、简化的中间结果:
(1)主矢
——大小:
;
方向:
,
。
(2)主矩
3、简化的最后结果:
(1)主矢
——[1]、
,合力,作用在
点;
[2]、
,合力,作用线距
点为
。
(2)主矢
——[1]、
,合力偶,与简化中心无关;
[2]、
,平衡,与简化中心无关。
4、平面任意力系的平衡
(1)平衡条件——
、
。
(2)平衡方程——[1]、基本式:
、
、
;
[2]、二矩式:
、
、
,
、
连线不垂直于
轴;
[3]、三矩式:
、
、
,
、
、
三点不得共线。
5、平面平行力系平衡方程:
(1)
、
,
轴不垂直力的作用线;(至少有一个力矩方程)
(2)
、
,
、
连线不与各力平行。
注
意点:(1)矩心应取在多个未知力的交点上;
(2)投影方程和力矩方程中的正负号;
(2)平衡方程的写法:
,不可写成
、
、
或
。
6、静定与超静定问题——比较未知量个数与独立平衡方程的个数。
7、平面简单桁架内力计算——(1)节点法(平面汇交力系)、(2)截面法(平面任意力系)
第四章、空间力系
教学目标:掌握空间力系的简化与平衡力系的求解方法,会计算物体的重心。
知识结构:
1、力在轴上的投影——直接投影法、间接(二次)投影法。
2、空间汇交力系——合成与平衡(三个独立方程)
3、力对点之矩、力对轴之矩——对点
,对轴
等;力对点的矩矢在过该点的轴上的投影等于力对该轴的矩。
4、空间力偶系——合成与平衡
5、空间任意力系的简化:
(1)中间结果:
[1]、主矢
——大小:
;
方向:
等。
[2]、主矩
(2)最后结果:
[1]、主矢
——[a]、
,合力,作用线过简化中心;
[b]、
、
,合力,作用线距
点为
;
[c]、
、
,力螺旋,中心轴过
点。
[2]、主矢
——[a]、
,合力偶,与简化中心无关;
[b]、
,平衡,与简化中心无关。
6、空间任意力系的平衡
(1)平衡条件——
、
。
(2)平衡方程——
、
、
、
、
、
。
(3)、空间平行力系平衡方程:
、
、
等
7、重心确定方法:
(1)利用对称性:在对称轴、对称面或对称中心上;
(2)分割法(负面积法):
等;——三角形的重心
、半圆的重心
(3)实验法:悬挂法,称重法。
第五章、摩擦
教学目标:能够熟练地分析有摩擦时物体的平衡问题并求解。
知识结构:
1、滑动摩擦力
(1)静滑动摩擦力——方向:与相对滑动趋势方向相反;
大小:
。
(2)动滑动摩擦力——方向:与相对滑动方向相反; 大小:
。
2、摩擦角与自锁
(1)摩擦角
——临界平衡状态时,全约束力与接触处公法线之间的夹角,或
。
(2)自锁——所有主动力合力的作用线与接触处公法线间的夹角小于摩擦角,物体静止的情况。
3、滚动摩阻——转向:与相对滚动趋势转向相反;
大小:
。
运动学
运动学是研究物体运动的的几何性质(轨迹、运动方程、速度和加速度等)的科学。
第六章、点的运动学
教学目标:能够熟练地计算点的位移、速度和加速度。
知识结构:
1、 研究内容——研究点相对某参考系的几何位置随时间变化的规律,包括点的运动轨迹、运动方程、速度和加速度。
2、 研究方法:
(1)矢量法——
、
、
(2)直角坐标法——
、
、
等
(3)自然法——
、
、
。
注
意点:(1)矢量法主要用于理论推导;
(2)直角坐标法是较为一般的方法。特别是点的运动轨迹未知的情形;
(3)自然法(弧坐标法)是针对点的运动轨迹已知的情形。运算简便,各量物理意义明确;
(4)
与
的区别。
第七章、刚体的简单运动
教学目标:能熟练计算定轴转动刚体的角速度、角加速度以及刚体内各点的速度和加速度,正确计算轮系的传动比。
知识结构:
1、刚体的平行移动(平移):
(1)定义:在刚体内任取一直线段,在运动过程中这条直线段始终与其初始位置平行;
(2)分类:若刚体内各点的轨迹为直线,则称为直线平移;
若刚体内各点的轨迹为平面曲线,则称为平面曲线平移;
若刚体内各点的轨迹为空间曲线,则称为空间曲线平移;
2、刚体的定轴转动:
(1)定义:刚体在运动时,其上或其扩展部分有两点保持不动。
(2)刚体定轴转动的整体运动描述:
[1]、转动方程——
;
[2]、角速度——
,
[3]、角加速度——
,
(3)定轴转动刚体上各点的运动描述:
[1]、运动方程——
,
是点到转轴的距离;
[2]、速度:
,
[3]、加速度:
,其中:
,
,
,
。
3、 轮系的传动比——主动轮I与从动轮II的角速度的比值
;正号表示两轮为同向转动,负号表示两轮为反向转动。
第八章、点的合成运动
教学目标:能正确选取动点、动系,分析三种运动,掌握速度和加速度的合成。
知识结构:
1、 研究同一点相对两个不同参考系的运动之间的关系。
2、 定性分析:
(1)动点——合成运动的研究对象;
(2)参考系——[1]、定参考系:习惯上把固结在地球上的参考系称为定系;
[2]、动参考系:把相对定系做运动的参考系称为动系;
(3)运动——[1]、绝对运动:动点相对定系的运动;
[2]、相对运动:动点相对动系的运动;
[3]、牵连运动:动系相对定系的运动——牵连点对定系的速度和加速度称为动点在该瞬时的牵连速度、牵连加速度。
3、定量分析:
(1)点的速度合成定理:
;
(2)点的加速度合成定理:
,
。
注
意点:动点、动系和定系的选择原则:
(1)动点、动系和定系必须分别属于三个不同的物体,否则绝对、相对和牵连运动中就缺少一种运动,不能成为合成运动;
(2)动点相对动系的相对运动轨迹易于直观判断(已知绝对运动和牵连运动求解相对运动的问题除外)。否则,会使相对加速度分析产生困难。
具体地,有:
[1]、两个不相关的动点,求二者的相对速度。
根据题意,选择其中之一为动点,动系为固结于另一点的平动坐标系;
[2]、运动刚体上有一动点,点作复杂运动。
该点取为动点,动系固结于运动刚体上。
[3]、机构传动,传动特点是在一个刚体上存在一个不变的接触点,相对于另一个刚体运动。
(a)导杆滑块机构:典型方法是动系固结于导杆,取滑块为动点。
(b)凸轮挺杆机构:典型方法是动系固结于凸轮,取挺杆上与凸轮接触点为动点。
(c)特殊问题,特点是相接触两个物体上的接触点位置都随时间而变化。此时,这连个物体的接触点都不宜选为动点,应选择满足前述选择原则的非接触点为动点。
第九章、刚体的平面运动
教学目标:能运用基点法、速度瞬心法和速度投影定理求解平面运动刚体上各点的速度和加速度。
知识结构:
1、刚体的平面运动——在运动中,刚体上的任意一点与某一固定平面的距离始终保持不变。
2、定性分析:(1)简化为平面图形在自身平面内的运动;
(2)平面运动可以分解为随基点的平移与绕基点的转动。
3、定量分析:(1)平面运动方程——
,
,
;
(2)基点法求平面图形内各点速度——
——速度投影定理:向
、
两点连线方向投影——
;
——速度瞬心法:取速度为零的
点为基点——
;
(3)基点法求平面图形内各点加速度——
。
注
意点:(1)车轮纯滚动问题,轮心加速度与角加速度之间的关系。
(2)机构运动学分析(连接点运动学分析)
[1]、若已知点的位置、时间的函数关系,可根据点的运动学,确定速度、加速度;
[2]、接触滑动——可根据合成运动的理论分析;(两个刚体)
[3]、铰链连接——可根据平面运动理论求解。(同一平面运动刚体)
动力学
动力学:研究物体的机械运动与作用力之间的关系。
第十章、质点动力学的基本方程
教学目标:能正确建立质点的运动微分方程。
知识结构:
动力学基本定律:
1、第一定律(惯性定律);
2、第二定律(质点动力学基本方程):
——质点运动微分方程:
;投影式***1、已知运动求力;2、已知力求运动;(3)混合问题。
3、第三定律(作用与反作用定律)。
第十一章、动量定理
教学目标:能熟练运用动量定理、质心运动定理及其守恒定律求解动力学问题。
知识结构:
1、质点动量——
(1)质点动量定理:[1]、微分形式——或;
[2]、积分形式——。
2、质点系动量——
或
(1)质点系动量定理:[1]、微分形式——或;
[2]、积分形式——。
(2)质心运动定理——。
3、冲量:(1)常力的冲量——;
(2)变力的冲量——。
注
意点:(1)质心运动定理的应用
——常用方法:[1]、求系统质心坐标;[2]、求导得质心加速度;[3]、利用质心运动定理求外力。
(2)动量守恒定律及质心运动守恒定律;
(3)各运动量均应是相对惯性参考系的绝对运动量。
第十二章、动量矩定理
教学目标:能熟练运用动量矩定理及其守恒定律求解动力学问题,会计算刚体定轴转动和平面运动的动力学问题。
知识结构:
1、质点对点
的动量矩——
。
2、质点系对点
的动量矩——
;对轴的动量矩——
。
(1)刚体平移——
;
(2)定轴转动——
。
3、质点系动量矩定理——;
——投影式:
。
4、刚体定轴转动微分方程——。
5、刚体对轴的转动惯量——
;
(1)平行轴定理——
;
(2)回转半径——
或
。
6、质点系相对质心的动量矩定理——。
7、刚体平面运动微分方程——、、或、、。
注
意点:
(1)动量矩定理的表达形式只适合于对固定点或固定轴,且其中的速度或角速度都是绝对速度或绝对角速度。对质心也成立时,其中的速度或角速度还可以是相对质心的速度或角速度。
(2)建立坐标系,在有一个固定轴的情况下一般取为角位移,角位移的正向确定后,角速度、角加速度以及力矩的方向均与角位移的正向相一致。
(3)注意动量矩守恒定律的应用。
(4)记住三个转动惯量:[1]、均质杆对一端的转动惯量——
;
[2]、均质杆对中心轴的转动惯量——
;
[3]、均质圆盘对中心轴的转动惯量——
。
(5)灵活运用动量定理、动量矩定理判断物体做何种运动,如P278,12-6,12-7。
第十三章、动能定理
教学目标:能熟练运动动能定理和机械能守恒定律求解动力学问题。
知识结构:
1、功——
(1)常力在直线运动中的功——
;
(2)重力的功——
;
(3)弹性力的功——;
(4)定轴转动刚体上的功——;
(5)平面运动刚体上力系的功——。
2、质点系的动能——
(1)平移刚体的动能——
;
(2)定轴转动刚体的动能——
;
(3)平面运动刚体的动能——
。
3、动能定理:(1)微分形式——;
(2)积分形式——。
4、功率方程——。
5、机械能守恒定律。
注
意点:一般情况下,需综合应用这些定理求解未知量。
(1)优选动能定理,动能定理取整个系统作为研究对象的机会多些。且若系统只有一个自由度,且为理想约束,应首先考虑使用动能定理求运动(但求不出约束力),再应用动量定理(质心运动定理)、动量矩定理求约束反力。
(2)对突减约束问题,一般宜采用平面运动微分方程求解。
(3)注意观察有无动量守恒、动量矩守恒,若有,则要充分利用这些条件。
第十四章、达朗贝尔原理(动静法)
教学目标:正确理解达朗贝尔原理,能熟练运用动静法求解质点和质点系的动力学问题。
知识结构:
1、达朗贝尔原理:
(1)惯性力—
;
(2)质点的达朗贝尔原理—
;
(3)质点系的达朗贝尔原理—
、
。
2、惯性力系的简化:
(1)刚体平移,向质心简化——
;
(2)刚体定轴转动,向转轴
上一点简化——
;
(刚体有质量对称平面且与转轴垂直)——
;
亦可向质心简化——
、
;
(3)刚体做平面运动,向质心简化——
;
(平行于质量对称平面)——
3、避免出现轴承动约束力的条件是——转轴通过质心,且刚体对转轴的惯性积等于零;或曰刚体的转轴应是刚体的中心惯性主轴。
注
意点:
(1)达朗贝尔原理常用于求解突减约束动力学问题;
(2)惯性力系取决于绝对加速度、绝对角加速度。
第十五章、虚位移原理
教学目标:会运用虚位移原理求解系统(非自由质点系)的平衡问题。
知识结构:
1、约束类型(了解);
2、虚位移——在某瞬时,质点系在约束允许的条件下,可能实现的任何无限小的位移;
3、虚功——力在虚位移中做的功
;
4、虚位移原理——对于具有理想约束的质点系,其平衡的充分必要条件是:作用在质点系的所有主动力在任何虚位移中所做虚功之和为零
或
。
注
意点:
1、对理想约束系统,常取整个系统为研究对象;
2、求各虚位移之间的关系
(1)几何法——根据主动力与虚位移的方向确定虚功的正负号、且要画出主动力作用点的虚位移;
(2)解析法——此时采用的虚功方程是它的解析式,即
其中
等是第
个力作用点坐标的变分,而
等是第
个力在相应坐标轴上的投影;
(3)虚速度法——虚速度之间的关系与实速度之间的关系是相同的,即可以根据运动学理论分析。
运动学公式
定轴转动刚体上一点的速度和加速度:(角量与线量的关系)
三.运动学解题步骤.技巧及注意的问题
1.分析题中运动系统的特点及系统中点或刚体的运动形式。
2.弄清已知量和待求量。
3.选择合适的方法建立运动学关系求解。
各种方法的步骤,技巧和使用中注意的问题详见每次习题课中的总结。
动力学公式
1. 动量定理
质点系动量定理的微分形式,即质点系动量的增量等于作用于质点系的外力元冲量的矢量和;或质点系动量对时间的导数等于作用于质点系的外力的矢量和.
质心运动定理
Mac = ∑F ≡ R
2. 动量矩定理:
平行移轴定理
刚体平面运动微分方程
三.动能定理
平面运动刚体的动能:
四. 达朗伯原理
对整个质点系,主动力系、约束反力系、惯性力系形式上构成平衡力系。这就是质点系的达朗伯原理。可用方程表示为:
用动静法求解动力学问题时,对平面任意力系,刚体平面运动可分解为
随基点(质点C)的平动:
绕通过质心轴的转动:
根据动静法,有
虚位移原理
在某瞬时,质点系在约束允许的条件下,可能实现的任何无限小的位移称为虚位移 .
力在虚位移中作的功称虚功.
对于具有理想约束的质点系,其平衡的充分必要条件是:作用于质点系的所有主动力在任何虚位移中所作的虚功的和等于零.
,