数量关系几何模块考查都逐渐增多,大小正方体构建的题目也时常出现。
题干:有边长为n厘米的正方体,现将它切割为边长为1厘米的小正方体。(有的时候反过来,用小的堆砌大的)。
问题:一般情况下将大正方体表面涂上颜色,围绕涂色的话题进行考查。
特征:此类题目接近现实生活,题意理解上没有多大难度,考生第一眼感觉放弃十分可惜。但如果平时积累不够,此类题目在考场上极容易做起来耗费时间且准确率不高。
要想快速做出此类题目,需要先熟练掌握以下几个问题:
1.大正方体有多少块小正方体构成?
2.大正方体单个面有多少块小正方形?
3.大正方体表面有多少块小正方形,涉及多少个小正方体?
4.三面涂色的小正方体有多少块?
5.两面涂色的小正方体有多少块?
6.只有一面被涂上色的小正方体有多少块?
7.表面没有被涂色的小正方体有多少块?
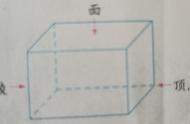
为了方便讲解这些问题,我们用一个大家非常熟悉的正方体为例,请看下图:

问题一:从魔方中很容易看出,每层上单排5个小正方体,整个一层5×5=25个,魔方共计5层,可得整个魔方有25×5=125个小正方体。即n三次方个。
问题二:从图中和问题一可得,单个面有25个小正方形,涉及25个小正方体。即n二次方个。
问题三:单个面有25个正方形,6个面一共150个正方形。但注意边缘的小正方体同时属于两个面,顶点的小正方体同时属于3个面。 此时有两种方法考虑。
1:先看黄色面,有25个小正方体,上面两个共计50个;再看蓝色面,去除上下两层(已被黄色面计算过了)还剩3×5=15个小正方体,两层共计为30个;最后看红色面,去除四周已经被计算过的,上下两层被黄色面计算过,左右两层被蓝色面计算过了,剩余3×3=9个,两层共计为18个。2n二次方 n(n-2) (n-2)的二次方。
表面可以被涂色颜色的小正方体:50 30 18=98个。
2:采取逆向思维。从图中可见,每行5个小正方体中的两端会被涂上颜色,中间3个不会,所有不漏出来的正方体为3的三次方为27个,在表面的涉及的小正方体为125-27=98个。
n三次方减(n-2)的三次方
问题四:从问题三和图中可得,三面涂色的小正方体只有顶点的8块。
问题五:从问题三和图中可得,两面涂色的小正方体是边缘的小正方体,每条边有3块,12条边共计36块。即12(n-2)个。
问题六:从问题三和图中可得,只有一面涂色的小正方体都位于表层中间,每个面上这种小正方体有9个,整个魔方6个面共计54个。即6倍(n-2)的二次方个。
问题七:从问题三和图中可得,整个魔方不漏出来的小正方体都属于没有涂色的,总计n3-(n-2)3个。
【真题演练】
1.1000个体积为1立方厘米的小正方体合在一起成为一个边长为10厘米的大正方体,大正方体表面涂油漆后,再分开为原来的小正方体,这些小正方体至少有一面被油漆涂过的数目是多少个?
A.490 B.488
C.484 D.480
2.一个木制正方体在表面涂上颜色,将它的每条棱三等分,然后从等分点将正方体割开,得到27个小正方体,将这些小正方体充分混合后,装入一个口袋,从这个口袋中随机取出两个小正方体,其中一个正方体只有一个面涂有颜色,另一个至少2个面涂有颜色的概率约为:
A.0.05 B.0.17
C.0.34 D.0.67
3.将一个8厘米×8厘米×1厘米的白色长方体木块的外表面涂上黑色颜料,然后将其切成64个棱长1厘米的小正方体,再用这些小正方体堆成棱长4厘米的大正方体,且使黑色的面向外露的面积尽量大,问大正方体的表面上有多少平方厘米是黑色的?
A.84 B.88
C.92 D.96
4.若干棱长为1cm的小正方体组成了一个棱长为8cm的大正方体,若此时将组成大正方体最外层的小正方体拿掉,然后将拿掉的小正方体所有面全部涂成黑色。若被涂黑的小正方体未从大正方体中拿掉,则被涂黑的面积将会减少多少?
A.1608 cm2 B.1392 cm2
C.428 cm2 D.128cm2
参考答案:BCBB