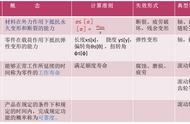
一个杆件(刚体)在平面可以由其上任一点A的坐标x和y,以及通过A点的垂线AB与横坐标轴的夹角等3个参数来决定,因此杆件具有3个自由度。

【计算公式】 F=3n-(2PL Ph ) n:活动构件数,PL:低副约束数Ph:高副约束数
计算平面机构自由度的注意事项:
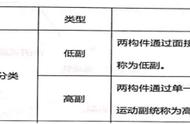
- 复合铰链 --两个以上的构件在同一处以转动副相联。复合铰链处理方法:如有K个构件在同一处形成复合铰链,则其转动副的数目为(k-1)个。
- 局部自由度:构件局部运动所产生的自由度,它仅仅局限于该构件本身,而不影响其他构件的运动。局部自由度常发生在为减小高副磨损而将滑动摩擦变为滚动磨擦所增加的滚子处。处理方法:在计算自由度时,从机构自由度计算公式中将局部自由度减去。


- 虚约束 --对机构的运动实际不起作用的约束。计算自由度时应去掉虚约束。虚约束都是在一定的几何条件下出现的。常见有以下几种情况:
- 两构件联接前后,联接点的轨迹重合。如:平行四边形机构,火车轮,椭圆仪。
- 两构件构成多个移动副,且导路平行。
- 两构件构成多个转动副,且同轴。
- 运动时,两构件上的两点距离始终不变。
- 对运动不起作用的对称部分。如多个行星轮
- 两构件构成高副,两处接触,且法线重合。如等宽凸轮
- 【注意】机构中出现虚约束是有条件的!虚约束一般有以下作用:改善机构受力情况;传递较大功率;
- 增加机构的刚度,如轴与轴承、机床导轨;使机构运动顺利,避免运动不确定,如车轮。