曲线拟合算法有哪些,什么是最佳拟合曲线

插值算法中，得到的多项式f(x)要经过所有样本点。但是如果样本点太多,那么这个多项式次数过高，会造成龙格现象。 尽管我们可以选择分段的方法避免这种现象，但是更多时候我们更倾向于得到一个确定的曲线，尽管这条曲线不能经过每一个样本点，但只要保证误差足够小即可，这就是拟合的思想。(拟合的结果是得到一个确定的曲线)

一个小例子：

对x，y数据绘制散点图，我们发现他们都散落在一个直线周围，此时我们想构造一个y=kx b的直线来当作拟合函数。

设这些样本点

我们设置的拟合曲线y=kx b

问题：k和b取何值时，样本点和拟合曲线最接近。

也就是说样本点和拟合函数值之间的差值最小

第一种定义：

第二种定义：

第一种有绝对值定义，不容易求导，因此计算比较复杂。

所以我们往往使用第二种定义，这也是最小二乘的思想。

为什么不用四次方？

（1）避免极端数据对拟合曲线的影响

（2）最小二乘法得到的结果和MLE极大似然估计一致

不用奇数次方的原因：误差会正负相抵。

设这些样本点，我们设置的拟合曲线

所以拟合值为

那么

令，现在就要找k、b使得L最小

(L在机器学习中常常成为损失函数，在回归中也常被称为残差平方和)

下面为的计算过程

参数k的计算过程

同理可得，

clear;clc load self_data1.mat plot(x,y,'o'); xlabel('x的值') ylabel('y的值') n = size(x,1); k = (n*sum(x.*y)-sum(y)*sum(x))/(n*sum(x.^2) - sum(x)*sum(x)); b = (sum(x.^2)*sum(y)-sum(x)*sum(x.*y))/(n*sum(x.^2) - sum(x)*sum(x)); hold on % 继续在之前的图上绘制 grid on % 显示网格线 f = @(x) k*x b fplot(f,[2.5,7]) legend('Sample data', 'Fitting function','location','southeast')

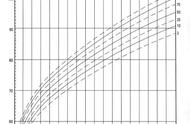
绘制出拟合函数的图像如下图所示，可以看到直线尽可能的接近于样本点。

拟合优度（可决系数）

总体平方和SST，Total sum of squares：

误差平方和SSE，The sum of squares：

回归平方和SSR，Sum of squares of the regression：

可以证明：SST = SSE SSR(证明过程在后面)

拟合优度：

R^2越接近1，说明误差平方和越接近于0，误差越小说明拟合越好。

（注意：只能用于拟合函数是线性函数时，拟合结果的评价）

线性函数和其他函数（例如复杂的函数）比较拟合的好坏，直接看SSE即可

未来我们会见到是个负数

总体平方和SST，Total sum of squares：

误差平方和SSE，The sum of squares：

回归平方和SSR，Sum of squares of the regression：

一阶导数条件：

首先我们要明白一个原则那就是，我们使用拟合函数的初衷就是要得到一个简单的拟合函数来刻画这些样本点，但是一味地追求的话，那岂不是使用插值多项式更好？因为插值多项式肯定会经过这些所有样本点，那么SSE就等于0，这样的话拟合函数就是插值多项式，但这违背了我们使用拟合函数的初衷。所以说，没有明确的说到底控制在什么范围内是最好的，这是一个涉及到取舍的问题。但原则是拟合函数越简单，拟合误差越小。

思考一下：是一个线性函数吗？

对于线性有两种解释，一种是对变量线性，也就是对x线性，很明显这里x是平方，所以对x来说肯定不是线性函数。

第二种是对参数线性，对于a和b来讲，此时函数是线性函数，且对参数线性，因为x是已知的样本点。

所以，需要注意，在拟合这里我们讨论的是对参数线性。

如何判断线性于参数的函数？

在函数中，参数仅以一次方出现，且不能创意或者除一其他任何参数，并且不能出现参数的复合函数形式。

例如，都不是线性函数，不能用

% 计算拟合优度 hat_y = k * x b; SST = sum((y - mean(y)).^2) SSE = sum((y - hat_y).^2) SSR = sum((hat_y - mean(y)).^2) SST-SSE-SSR % 计算存在误差，不然应该是等于0的 R_2 = 1 - SSE/SST % 最终结果0.9635

中心化（标准化）公式