ansys计算结果不一样,ansys怎么重新计算结果

右侧长方体的Z向变形分布如下图所示，其左端也为受压的Z向位移，其数值为-0.49123mm。

右侧长方体的轴向应力（Z向正应力）分布如下图所示，其数值也为-196.49MPa（压应力）。

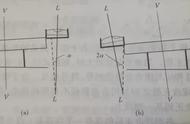
在这个算例中，右侧长方体的左端面在界面调整后与左侧长方体发生1.0mm的干涉，由于没有施加任何强迫位移，因此这种情况相当于计算由于界面干涉引起的过盈配合。

根据过盈配合的概念可知，左侧长方体右端面的Z向位移为0.5mm且处于受压状态，右侧长方体左端面的Z向位移则为-0.5mm，也处于受压的状态。通过界面调整方法计算的端部位移为±0.49123mm。实体中的轴向压应变为0.5mm/500mm=0.001，轴向应力理论值为-200MPa，计算结果为-196.49Pa，相对误差均不超过2%。

在ANSYS Workbench中，还可以利用基于Remote Point的Constraint Equation来计算过盈配合应力。我们还是以上面相同的算例来介绍有关的实现方法。

如下图所示，两个尺寸为0.1×0.1×0.5m的长方体，材质为结构钢，E=2e11Pa，泊松比为0。

在这里与前面一种方法有一处细微差别，如下面的局部放大图所示，右侧长方体的左侧面与左侧长方体发生了1mm的几何干涉。