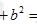1.复习直角三角形的相关知识,归纳并掌握直角三角形的性质和判定;
2.学习并掌握勾股定理及其逆定理,能够运用其解决问题.(重点,难点)
一、情境导入
古埃及人曾经用下面的方法画直角:将一根长绳打上等距离的13个结,然后按如图所示的方法用桩钉钉成一个三角形,他们认为其中一个角便是直角.你知道这是什么道理吗?
二、合作探究
探究点一:直角三角形的性质与判定
【类型一】 判定三角形是否为直角三角形
具备下列条件的△ABC中,不是直角三角形的是( )
A.∠A+∠B=∠C
B.∠A-∠B=∠C
C.∠A∶∠B∶∠C=1∶2∶3
D.∠A=∠B=3∠C
解析:由直角三角形内角和为180°求得三角形的每一个角的度数,再判断其形状.A中∠A+∠B=∠C,即2∠C=180°,∠C=90°,为直角三角形,同理,B,C中均为直角三角形,D选项中∠A=∠B=3∠C,即7∠C=180°,三个角没有90°角,故不是直角三角形.故选D.
方法总结:在判定一个三角形是否为直角三角形时要注意直角三角形中有一个内角为90°.
【类型二】 直角三角形的性质的应用
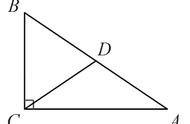
如图①,△ABC中,AD⊥BC于D,CE⊥AB于E.
(1)猜测∠1与∠2的关系,并说明理由.
(2)如果∠A是钝角,如图②,(1)中的结论是否还成立?
解析:(1)根据垂直的定义可得△ABD和△BCE都是直角三角形,再根据直角三角形两锐角互余可得∠1+∠B=90°,∠2+∠B=90°,从而得解;(2)根据垂直的定义可得∠D=∠E=90°,然后求出∠1+∠4=90°,∠2+∠3=90°,再根据∠3、∠4是对顶角解答即可.
解:(1)∠1=∠2.∵AD⊥BC,CE⊥AB,∴△ABD和△BCE都是直角三角形,∴∠1+∠B=90°,∠2+∠B=90°,∴∠1=∠2;
(2)结论仍然成立.理由如下:∵BD⊥AC,CE⊥AB,∴∠D=∠E=90°,∴∠1+∠4=90°,∠2+∠3=90°,∵∠3=∠4(对顶角相等),∴∠1=∠2.
方法总结:本题考查了直角三角形的性质,主要利用了直角三角形两锐角互余,同角或等角的余角相等的性质,熟记性质是解题的关键.
探究点二:勾股定理
【类型一】 直接运用勾股定理
已知:如图,在△ABC中,∠ACB=90°,AB=13cm,BC=5cm,CD⊥AB于D.求:
(1)AC的长;
(2)S△ABC;
(3)CD的长.
解析:(1)由于在△ABC中,∠ACB=90°,AB=13cm,BC=5cm,根据勾股定理即可求出AC的长;(2)直接利用三角形的面积公式即可求出S△ABC;(3)根据CD·AB=BC·AC即可求出CD.
解:(1)∵在△ABC中,∠ACB=90°,AB=13cm,BC=5cm,∴AC==12cm;
(2)S△ABC=CB·AC=30cm2;
(3)∵S△ABC=AC·BC=CD·AB,∴CD==cm.
方法总结:解答此类问题,一般是先利用勾股定理求出第三边,利用两种方法表示出同一个直角三角形的面积,然后根据面积相等得出一个方程,再解这个方程即可.
【类型二】 分类讨论思想在勾股定理中的应用
在△ABC中,AB=15,AC=13,BC边上的高AD=12,试求△ABC周长.
解析:本题应分两种情况进行讨论:(1)当△ABC为锐角三角形时,在Rt△ABD和Rt△ACD中,运用勾股定理可将BD和CD的长求出,两者相加即为BC的长,从而可将△ABC的周长求出;(2)当△ABC为钝角三角形时,在Rt△ABD和Rt△ACD中,运用勾股定理可将BD和CD的长求出,两者相减即为BC的长,从而可将△ABC的周长求出.
解:此题应分两种情况进行讨论:
(1)当△ABC为锐角三角形时,在Rt△ABD中,BD===9,在Rt△ACD中,CD===5,∴BC=BD+CD=5+9=14,∴△ABC的周长为15+13+14=42;
(2)当△ABC为钝角三角形时,在Rt△ABD中,BD===9.在Rt△ACD中,CD===5,∴BC=9-5=4,∴△ABC的周长为15+13+4=32.
∴当△ABC为锐角三角形时,△ABC的周长为42;当△ABC为钝角三角形时,△ABC的周长为32.
方法总结:在题目未给出具体图形时,应考虑三角形是锐角三角形还是钝角三角形,凡符合题设的情况都要考虑,体现了分类讨论思想,这是解无图几何问题的常用方法.
探究点三:勾股定理的逆定理
【类型一】 判断三角形的形状
如图,正方形网格中有△ABC,若小方格边长为1,则△ABC的形状为( )
A.直角三角形
B.锐角三角形
C.钝角三角形
D.以上答案都不对
解析:∵正方形小方格边长为1,∴BC==2,AC==,AB==.在△ABC中,∵BC2+AC2=52+13=65,AB2=65,∴BC2+AC2=AB2,∴△ABC是直角三角形.故选A.
方法总结:要判断一个角是不是直角,先要构造出三角形,然后知道三条边的大小,用较小的两条边的平方和与最大的边的平方比较,如果相等,则三角形为直角三角形;否则不是.
【类型二】 利用勾股定理的逆定理证明垂直关系
如图,在正方形ABCD中,AE=EB,AF=AD,求证:CE⊥EF.
证明:连接CF,设正方形的边长为4.∵四边形ABCD为正方形,∴AB=BC=CD=DA=4.∵点E为AB中点,AF=AD,∴AE=BE=2,AF=1,DF=3.由勾股定理得EF2=12+22=5,EC2=22+42=20,FC2=42+32=25.∵EF2+EC2=FC2,∴△CFE是直角三角形,∴∠FEC=90°,即EF⊥CE.
方法总结:利用勾股定理的逆定理可以判断一个三角形是否为直角三角形,所以此定理也是判定垂直关系的一个主要方法.
【类型三】 运用勾股定理的逆定理解决面积问题
如图,在四边形ABCD中,∠B=90°,AB=8,BC=6,CD=24,AD=26,求四边形ABCD的面积.
解析:连接AC,根据已知条件运用勾股定理的逆定理可证△ACD为直角三角形,然后代入三角形面积公式将△ABC和△ACD这两个直角三角形的面积求出,两者面积相加即为四边形ABCD的面积.
解:连接AC,∵∠B=90°,∴△ABC为直角三角形.∵AC2=AB2+BC2=82+62=102,∴AC=10.在△ACD中,∵AC2+CD2=100+576=676,AD2=262=676,∴AC2+CD2=AD2,∴△ACD为直角三角形,且∠ACD=90°,∴S四边形ABCD=S△ABC+S△ACD=×6×8+×10×24=144.
方法总结:此题将求四边形面积的问题转化为求两个直角三角形面积和的问题,既考查了对勾股定理逆定理的掌握情况,又体现了转化思想在解题时的应用.
探究点四:互逆命题与互逆定理
写出下列各命题的逆命题,并判断其逆命题是真命题还是假命题.
(1)两直线平行,同旁内角互补;
(2)垂直于同一条直线的两直线平行;
(3)相等的角是内错角;
(4)有一个角是60°的三角形是等边三角形.
解析:分别找出各命题的题设和结论将其互换即可.
解:(1)同旁内角互补,两直线平行.真命题;
(2)如果两条直线平行,那么这两条直线垂直于同一条直线(在同一平面内).真命题;
(3)内错角相等.假命题;
(4)等边三角形有一个角是60°.真命题.
方法总结:一个定理不一定有逆定理,只有当它的逆命题为真命题时,它才有逆定理.
三、板书设计
1.直角三角形的性质与判定
直角三角的两个锐角互余;有两个角互余的三角形是直角三角形.
2.勾股定理及勾股定理的逆定理
直角三角形两条直角边的平方和等于斜边的平方;如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
本节课充分发挥了学生动手操作能力、分类讨论能力、交流能力和空间想象能力,让学生充分体验到了数学思考的魅力和知识创新的乐趣,突显教学过程中的师生互动,使学生真正成为主动学习者.
,